Segment Tree Beats 学习笔记
前置知识:线段树
简要介绍
区间取 min/max 问题
先引入一个简单的问题:给定一个数列,你需要支持区间取 \(\min\),区间求和。怎么做?
普通的线段树只能支持区间求和,不能支持区间取 \(\min\),如果每次修改都暴力递归到叶子节点,时间复杂度就会爆炸。
显然有一个可行的剪枝:维护一下当前区间最大值,如果最大值比我要取 \(\min\) 的那个数还要小,那就直接返回,不用继续递归。
进一步考虑,维护一下 严格 次大值。如果我要取 \(\min\) 的那个数比最大值小,但是比次大值大,那我们就只修改最大值。这个应该很好实现,打个标记然后 pushdown 即可。
现在来证明复杂度是 \(O(q\log n)\) 的。
考虑下面一颗线段树,把我们维护的区间最大值标记在节点上:
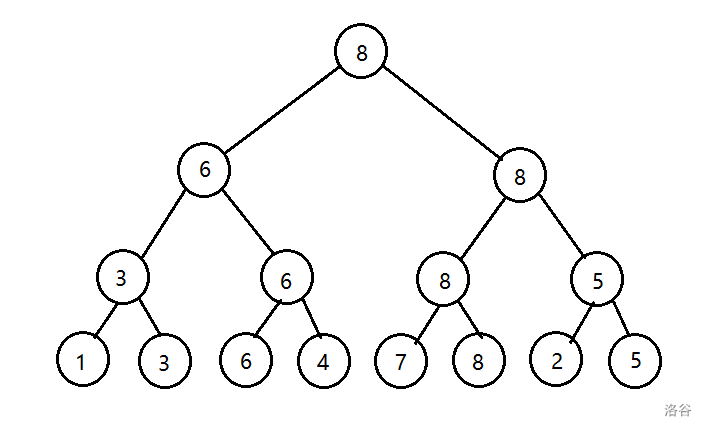
对于相同的权值,我们只取最上面的那个节点:
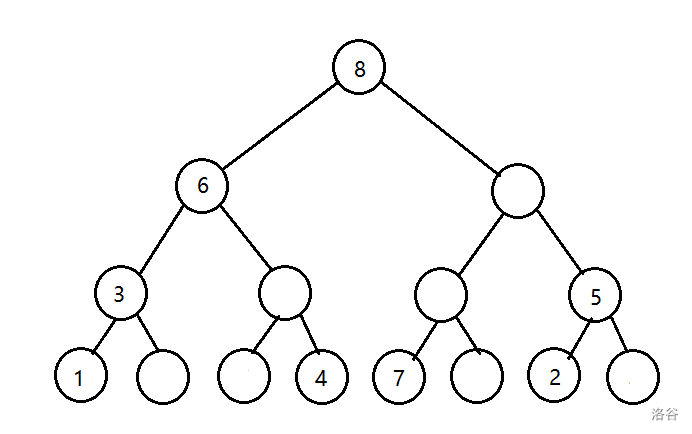
那么有个性质,就是一个节点的区间最大值就是这个节点的权值,次大值是它儿子权值的最大值。
现在,我们将一个区间 \([l,r]\) 与 \(v\) 取 \(\min\)。我们把 \(v\) 看作一个标记,这可能会将一些节点的权值修改为 \(v\),我们把这次操作所产生的标记记为同一类。当我们暴力递归的时候,至少会存在一类标记大于 \(v\),也就是至少会有 一类标记 被清除。
每次操作都会新增一类标记,每类标记的个数最多只有 \(\log n\) 个。所以均摊下来总时间复杂度为 \(O(q\log n)\)。
更严谨的证明可以到文末看吉老师的论文。
如果加上了类似区间加的操作,时间复杂度肯定不会超过 \(O(q\log^2 n)\),但实际上跑的跟 \(O(q\log n)\) 差不多。
历史最大值
先来个简单一点的问题:给你一个序列,你需要支持区间加,区间查最大值,区间查历史最大值。
对于前两个操作,我们对区间加打个 \(\text{tag}\),维护一下区间最大值,每次下传标记就给区间最大值加上 \(\text{tag}\) 就行了。
然后来看一下历史最大值怎么维护。对于 \(\text{pushup}\),直接对左右儿子取 \(\max\) 即可,重点是 \(\text{pushdown}\)。
在维护当前节点标记的时候,可能会发生如下操作:\(+5\),\(+4\),\(-3\),最终标记上的值就是 \(+5+4-3=+6\)。而在这期间某个时刻,这个标记达到了 \(+5+4=+9\),比最终的 \(+6\) 要大,所以历史最大值应该更可能是在 \(+9\) 的时候取到,而不是 \(+6\)。
所以除了维护区间加的标记,还需要维护 这个标记的历史最大值,用于区间历史最大值的更新。
于是在下传的时候,我们将区间历史最大值与原本区间的值 + 标记历史最大值取个 \(\max\) 就行了。代码如下:
void addtag(ll x,ll t1,ll t2){//t1为区间加的标记,t2为标记历史最大值
his[x]=max(his[x],maxx[x]+t2);
histag[x]=max(histag[x],tag[x]+t2);
maxx[x]+=t1;
tag[x]+=t1;
}
这就是最基本的历史最值问题,但当它与一些奇奇怪怪的操作(比如前面的区间取最值问题)结合起来的时候,一切都会变的复杂起来。
一些题目
CPU 监控
历史最值入门题目,虽然比较难写,但可以说是这类题目中最好写的一题了。
相比于前面的例题,这题多了一个区间赋值的操作。所以要多记录两个 \(\text{tag}\),表示覆盖的值和覆盖的历史最大值。
注意一旦出现覆盖,那么区间加的 \(\text{tag}\) 就没用了,以后的区间加要标记在区间赋值的 \(\text{tag}\)。
线段树 3
这题就是将前面讲的两种操作合并在了一起。按照惯例,区间取 \(\min\) 需要维护区间最大值与次大值,历史最值需要维护区间历史最大值,同时还要维护区间和。
对于 \(\text{pushdown}\),我们只需要维护加法标记,最大值加法标记,以及对应的历史最大值。
代码会很难写,细节很多,但是熟练就好了。
Cartesian Tree
前两题写吐了,就来做点小清新题吧。
看看大根笛卡尔树有什么性质:中序遍历为原序列顺序,父亲节点权值比儿子大。那么忽略权值 \(\leq k\) 的限制,假设 \(i\) 左边第一个权值比 \(i\) 大的位置为 \(l_i\),右边第一个权值比 \(i\) 大的位置为 \(r_i\),\(i\) 子树对应到原序列的区间就是 \((l_i,r_i)\)。所有点的子树和就是 \(\displaystyle\sum_{i=1}^{n}{r_i-l_i-1}\)。
将 \(l_i\) 和 \(r_i\) 分开计算,我们现在要求所有权值 \(\leq k\) 的点的 \(r_i\) 之和(\(l_i\) 同理)。因为权值互不相同,所以将序列上的数按权值从小到大加入。假设我们已经计算完 \(< k\) 的 \(r_i\),现在加入一个数,其位置为 \(pos\),权值为 \(k\),那么这个数的 \(r_i\) 就是 \(k+1\)。因为它比前面加入的数都要大,所以在 \(pos\) 左边的数的 \(r_i\) 都不能超过它,也就是将 \(1 \sim pos-1\) 的 \(r_i\) 跟 \(pos\) 取 \(\min\)。因为在 \(pos\) 的位置新插了一个数,所以 \(pos+1 \sim n\) 的 \(r_i\) 都要 \(+1\)。
现在问题变成了单点修改,区间取 \(\min\),区间加,全局求和,用 Segment Tree Beats 解决,时间复杂度 \(O(n\log^2 n)\)。
Stations
直接维护广播站能被多少广播站传播显然十分麻烦,考虑维护一个广播站能传播到哪些地方。找到第 \(i\) 个广播站右边第一个比它高的广播站位置,记为 \(pos_i\),那它能传播到的广播站就是 \([i,\min(w_i,pos_i-1)]\),我们称 \(r_i=\min(w_i,pos_i-1)\)。
对于 \(1\) 操作,先把 \(r_i\) 赋为 \(g\)。因为它现在是最高的广播站了,所以它左边广播站的 \(r_i\) 都不能超过它,于是对左边的 \(r_i\) 与 \(i\) 取 \(\min\),用 Segment Tree Beats 即可。
对于 \(2\) 操作,计算有多少个 \([i,r_i]\) 包含它。再建一棵线段树,对每一个 \(i\),就在 \([i,r_i]\) 加 \(1\),然后单点查询。至于如何维护,直接在操作 \(1\) 的过程中更改即可。
具体来说,在操作 \(1\) 的时候,我们要修改某些节点的最大值,比如将 \(maxx\) 修改为 \(v\),那就在第二颗线段树上把 \([v+1,maxx]\) 减去最大值个数就行了。
Karen and Cards
设三元组为 \((x,y,z)\),一个暴力的想法是枚举前两维,然后计算合法的第三维个数。
先枚举 \(x \in [1,p]\),然后枚举 \(y\)。如果发现存在 \(i\) 使得 \(a_i \geq x\) 且 \(b_i \geq y\),那么无论 \(z\) 是什么它都是不合法的。所以 \(y > \displaystyle\max_{a_i \geq x}{b_i}\)。
再考虑 \(z\),如果存在 \(i\) 使得 \(a_i \geq x\),那么 \(z > c_i\),否则无论如何都不合法,所以 \(z > \displaystyle\max_{a_i \geq x}{c_i}\)。同理,\(z > \displaystyle\max_{a_i < x,b_i \geq y}{c_i}\),故 \(z > \max(\displaystyle\max_{a_i \geq x}{c_i},\displaystyle\max_{a_i < x,b_i \geq y}{c_i})\),合法个数为 \(r-\max(\displaystyle\max_{a_i \geq x}{c_i},\displaystyle\max_{a_i < x,b_i \geq y}{c_i})\)。
如果只枚举一层,设 \(Bmax=\displaystyle\max_{a_i \geq x}{b_i},Cmax=\displaystyle\max_{a_i \geq x}{c_i},f_y=\displaystyle\max_{a_i < x,b_i \geq y}{c_i}\),则前两个可以通过倒序枚举 \(x\) 预处理。至于 \(f_y\),可以从小到大枚举 \(x\),把 \(a_i=x\) 的三元组一个个加进去,然后将 \(y \leq b_i\) 的 \(f_y\) 对 \(c_i\) 取 \(\max\)。
区间取 \(\max\) 问题,直接套 Segment Tree Beats 即可。至于答案求和,可以把 \(\max\) 拆开,在线段树上二分第一个 \(f_y\leq Cmax\) 的位置,然后再区间求和。
参考资料:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号