网络流24题

已做

•   P2756

•   P3254

•   P4014

•   P4009

未做

•   P4011

•   P2761

•   P4016

•   P3358

•   P2774

•   P4015

•   P2770

•   P2754

•   P2762

•   P4012

•   P1251

•   P2763

•   P2766

•   P3355

•   P3357

•   P4013

•   P2765

•   P3356

•   P2764

•   P2775

P4011

留坑

P2756

Link

裸的网络流，当然也可以用二分图匹配

首先讲讲怎么建图（好像也不用怎么讲）

就以样例为例，有5个外籍飞行员（编号\(1\)_{$5$）和5个英国飞行员（编号$6$}\(10\)），对于每一个可以配对的飞行员，就在他们两个之间连一条边。然后源点\(s\)连所有外籍飞行员，汇点\(t\)连英国飞行员，这样就保证了一定是外籍飞行员和英国飞行员搭配。因为每个飞行员只能配对一个飞行员，所以不妨让每条边的最大容量都为\(1\)。于是图就建完了。

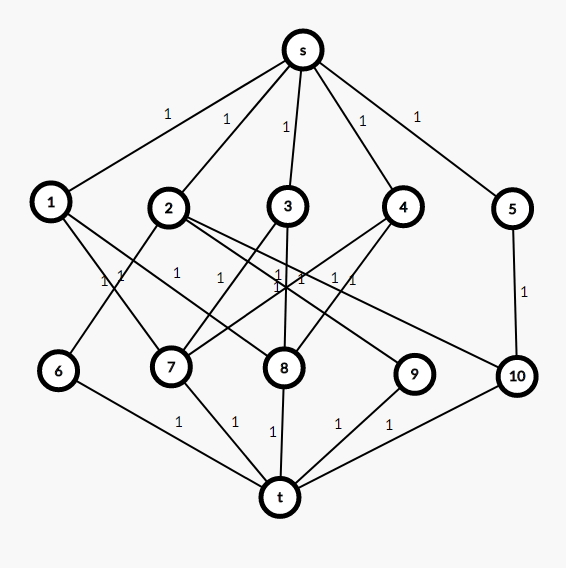
由于每条边的最大容量都为\(1\)，所以如果一个流能从\(s\)流到\(t\)，那么流最终的大小必定为\(1\)，所以图的最大流就是能派出最多的飞机数量。然后在跑完最大流后遍历每一条边，看它的流是否大于\(0\)（从高处流到低处），如果是就说明起点和终点最终可以匹配，就输出这条边的起点和终点。值得一提的是，因为题目只要求问飞行员的匹配情况，所以得排除连向\(s\)和\(t\)的边。

代码：

#include<bits/stdc++.h>
using namespace std;
using namespace my_std;
ll m,n,x,y,s,t,head[10001],dep[10001],cnt=1,ans=0;
struct node{
	ll nxt,to,w;
}e[10001];
void add(ll u,ll v,ll w){
	e[++cnt].nxt=head[u];
	e[cnt].to=v;
	e[cnt].w=w;
	head[u]=cnt;
}
bl bfs(){
	memset(dep,0,sizeof(dep));
	queue<ll> q;
	q.push(s);
	dep[s]=1;
	while(!q.empty()){
		ll u=q.front();
		q.pop();
		go(u){
			ll v=e[i].to;
			if(e[i].w&&!dep[v]){
				dep[v]=dep[u]+1;
				q.push(v);
			} 
		}
	}
	return dep[t];
}
ll dfs(ll u,ll flow){
	if(u==t||(!flow)) return flow;
	ll k,res=0;
	go(u){
		ll v=e[i].to;
		if(e[i].w&&dep[v]==dep[u]+1){
			k=dfs(v,min(flow,e[i].w));
			if(!k) dep[v]=maxinf;
			e[i].w-=k;
			e[i^1].w+=k;
			res+=k;
			flow-=k;
		}
	}
	return res;
}
int main(){
	m=read();
	n=read();
	x=read();
	y=read();
	s=0;
	t=n+1;
	fr(i,1,m){
		add(s,i,1);
		add(i,s,0);
	}
	fr(i,m+1,n){
		add(i,t,1);
		add(t,i,0);
	}
	while(x!=-1||y!=-1){
		add(x,y,1);
		add(y,x,0);
		x=read();
		y=read();
	}
	while(bfs()) ans+=dfs(s,maxinf);
	writeln(ans);
	for(ll i=2;i<=cnt;i+=2){
		if(e[i^1].w&&e[i^1].to!=s&&e[i].to!=t){
			writesp(e[i^1].to);
			writeln(e[i].to);
		}
	}
}

P2761

留坑

P4016

留坑

P3358

留坑

P4014

Link

（打完最大流裸题就来打费用流裸题的蒟蒻LZY是屑）

裸费用流（也可以用二分图最佳完美匹配来做）

题目大意：有\(n\)个人，\(n\)项工作，每个人都对应一项不同的工作，每个人做对应的工作都有一个对应的效益，求效益的最大/最小值。

显然要用到费用流。既然要用网络流做，那么常规地就把源点\(s\)和每个人（\(1\)_{$n$）连起来，因为每个人只能参加$1$项工作，所以就设最大容量为$1$，花费为$0$。再把每个人和每个工作（$n$+$1$}\(2n\)）连起来，最大容量为\(1\)，因为每个人做工作都有一个效率，所以边的花费就为对应的人做对应的工作的效益。最后把每项工作与汇点\(t\)连起来，最大流量为\(1\)，花费为\(0\)，跑一遍最小费用最大流和最大费用最小流就行了。（图中间很乱，凑合着看吧）

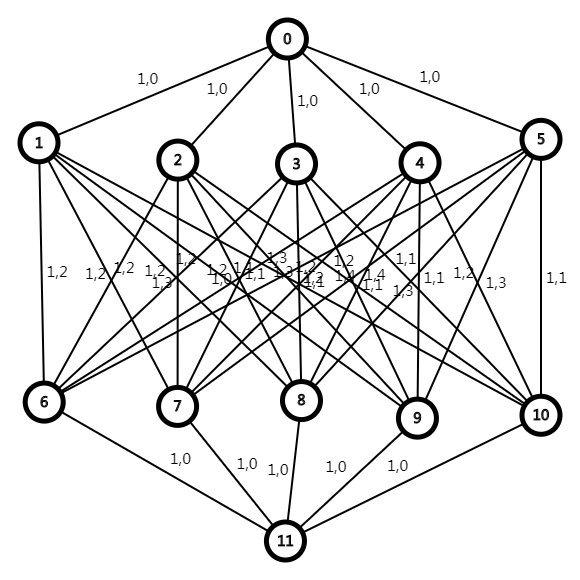
当然，我在求最大费用最大流的时候用了一些小技巧（至少不会使代码那么长QwQ），就是在求完最小费用后重新建一次边，但是把边原来的花费都变为它的相反数，这样原来较大的就变为较小的了。然后再用新的图跑一次最小费用最大流，输出答案的相反数就可以啦。

代码：

#include<bits/stdc++.h>
using namespace std;
using namespace my_std;
ll n,c[101][101],s,t,head[100001],cnt=1,dist[100001],ansc=0;
bl ck[100001];
struct node{
	ll nxt,to,flow,cost;
}e[200002];
void add(ll x,ll y,ll f,ll c){
	e[++cnt].nxt=head[x];
    e[cnt].to=y;
	e[cnt].flow=f;
	e[cnt].cost=c;
	head[x]=cnt;
}
bool spfa(){
    memset(ck,0,sizeof(ck));
    fr(i,0,2*n+1) dist[i]=maxinf;
	dist[t]=0;
	ck[t]=1;
    deque<ll> q;
	q.push_back(t);
    while(!q.empty()){
        ll u=q.front();
		q.pop_front();
        go(u){
        	ll v=e[i].to;
        	if(e[i^1].flow&&dist[v]>dist[u]-e[i].cost){
            	dist[v]=dist[u]-e[i].cost;
            	if(!ck[v]){
            	    ck[v]=1;
           	    	if(!q.empty()&&dist[q.front()]>dist[v]) q.push_front(v);
					else q.push_back(v);
            	}
        	}
        }
        ck[u]=0;
    }
    return dist[s]<maxinf;
}
ll dfs(ll u,ll sum){
    if(u==t){
		ck[t]=1;
		return sum;
	}
	ck[u]=1;
    ll k,res=0;
	go(u){
		ll v=e[i].to;
		if(!ck[v]&&e[i].flow&&(dist[u]-e[i].cost)==dist[v]){
        	k=dfs(e[i].to,min(sum-res,e[i].flow));
        	if(k){
        		ansc+=k*e[i].cost;
				res+=k;
				e[i].flow-=k;
				e[i^1].flow+=k;
        	}
        	if(res==sum) break;
    	}
	}
    return res;
}
void zkw(){
    while(spfa()){
        ck[t]=1;
        while(ck[t]){
            memset(ck,0,sizeof(ck));
            dfs(s,maxinf);
        }
    }
    return;
}
void init(){
	memset(e,0,sizeof(e));
	ansc=0;
	cnt=1;
	memset(ck,0,sizeof(ck));
	memset(head,0,sizeof(head));
}
int main(){
	n=read();
	s=0;
	t=2*n+1;
	fr(i,1,n){
		add(s,i,1,0);
		add(i,s,0,0);
	}
	fr(i,n+1,2*n){
		add(i,t,1,0);
		add(t,i,0,0);
	}
	fr(i,1,n){
		fr(j,1,n){
			c[i][j]=read();
			add(i,j+n,1,c[i][j]);
			add(j+n,i,0,-c[i][j]);
		}
	}
	zkw();
	writeln(ansc);
	init();
	fr(i,1,n){
		add(s,i,1,0);
		add(i,s,0,0);
	}
	fr(i,n+1,2*n){
		add(i,t,1,0);
		add(t,i,0,0);
	}
	fr(i,1,n){
		fr(j,1,n){
			add(i,j+n,1,-c[i][j]);
			add(j+n,i,0,c[i][j]);
		}
	}
	zkw();
	write(-ansc);
}

P2774

留坑

P4009

Link

（突然感觉做网络流题都是套个模板然后重新建边就可以了）

题目大意：一个\(n \times n\)的方格，要从\((1,1)\)开车到\((n,n)\)，每走一格都会耗一格油。车辆原来有\(k\)格油，然后一些位置会有加油站，到达这个位置就要花费\(A\)的价格加至\(k\)格油，如果没加油站也可以花\(C\)价格建一个（不包括加油费用）。如果往回走也要花\(B\)价格。

看到费用，那么肯定就是费用流了。很容易想到把每一格与相邻的格子连边，但是却很难考虑油量这个变量，我们没办法去求经过一段路程（甚至往回走）并且加过几次油后的油量。所以我们得思考另一种建图方式。既然不能求油量，不如直接把油量记录到图里面去，所以整个图就被分成了\(0\)~\(k\)层，其中第\(i\)层表示目前的油量。因为我们只有一辆车，且路线不重复（如果重复那肯定不是最优的），所以就默认每条边的最大容量为\(1\)。

一开始出发的油量肯定是\(k\)，所以将源点\(s\)与第\(k\)层的\((1,1)\)连边，费用为\(0\)，因为题目只要求到达\((n,n)\)，没有说到达时的油量限制，所以就将每一层的\((n,n)\)都与汇点\(t\)连边，费用也为\(0\)。接下来我们考虑加油的情况。第一种就是所在的这个点\((x,y)\)有一个加油站且油不是满的，因为是强制性消费，所以直接将这个点连向第\(k\)层同一位置的点，费用为\(A\)。至于第二种情况，因为费用要尽可能的小，所以就只用在油量为\(0\)的情况下与第\(k\)层同一个点连一条费用为\(A+C\)的边（注意，题目说\(C\)的价格不包括加油费用）。然后就让每个点与右边或下边相邻的点连一条费用为\(0\)的点，与上边或左边的点连一条费用为\(B\)的点。

自我感觉这建图有一点难想到，但是仔细思考就会发现还是常规的建图方法。注意：空间不要嫌大，要多开一点。

代码：

#include<bits/stdc++.h>
#define maxn 900009
using namespace std;
using namespace my_std;
ll n,k,a,b,c,s,t,head[maxn],cnt=1,dist[maxn],ans=0;
bl ck[maxn],pd[101][101];
struct node{
	ll nxt,to,flow,cost;
}e[maxn];
ll g(ll oil,ll xx,ll yy){
	return oil*n*n+(xx-1)*n+yy;
}
void add(ll x,ll y,ll f,ll c){
	e[++cnt].nxt=head[x];
    e[cnt].to=y;
	e[cnt].flow=f;
	e[cnt].cost=c;
	head[x]=cnt;
}
bool spfa(){
    memset(ck,0,sizeof(ck));
    fr(i,s,t) dist[i]=maxinf;
	dist[t]=0;
	ck[t]=1;
    deque<ll> q;
	q.push_back(t);
    while(!q.empty()){
        ll u=q.front();
		q.pop_front();
        go(u){
        	ll v=e[i].to;
        	if(e[i^1].flow&&dist[v]>dist[u]-e[i].cost){
            	dist[v]=dist[u]-e[i].cost;
            	if(!ck[v]){
            	    ck[v]=1;
           	    	if(!q.empty()&&dist[v]<dist[q.front()]) q.push_front(v);
					else q.push_back(v);
            	}
        	}
        }
        ck[u]=0;
    }
    return dist[s]<maxinf;
}
ll dfs(ll u,ll sum){
    if(u==t){
		ck[t]=1;
		return sum;
	}
	ck[u]=1;
    ll k,res=0;
	go(u){
		ll v=e[i].to;
		if(!ck[v]&&e[i].flow&&(dist[u]-e[i].cost)==dist[v]){
        	k=dfs(e[i].to,min(sum-res,e[i].flow));
        	if(k){
        		ans+=k*e[i].cost;
				res+=k;
				e[i].flow-=k;
				e[i^1].flow+=k;
        	}
        	if(res==sum) break;
    	}
	}
    return res;
}
void zkw(){
    while(spfa()){
        ck[t]=1;
        while(ck[t]){
            memset(ck,0,sizeof(ck));
            dfs(s,maxinf);
        }
    }
    return;
}
int main(){
	n=read();
	k=read();
	a=read();
	b=read();
	c=read();
	s=0;
	t=(k+1)*n*n+1;
	fr(i,1,n) fr(j,1,n) pd[i][j]=read();
	add(s,g(k,1,1),1,0);
	add(g(k,1,1),s,0,0);
	fr(i,0,k){
		add(g(i,n,n),t,1,0);
		add(t,g(i,n,n),0,0);
	}
	fr(oil,0,k){
		fr(x,1,n){
			fr(y,1,n){
				if(x==n&&y==n){
					add(g(oil,n,n),t,1,0);
					add(t,g(oil,n,n),0,0);
				}
				else if(pd[x][y]&&oil!=k){
					add(g(oil,x,y),g(k,x,y),1,a);
					add(g(k,x,y),g(oil,x,y),0,-a);
				}
				else if(!oil){
					add(g(oil,x,y),g(k,x,y),1,a+c);
					add(g(k,x,y),g(oil,x,y),0,-a-c);
				}
				else{
					if(x+1<=n){
						add(g(oil,x,y),g(oil-1,x+1,y),1,0);
						add(g(oil-1,x+1,y),g(oil,x,y),0,0);
					}
					if(y+1<=n){
						add(g(oil,x,y),g(oil-1,x,y+1),1,0);
						add(g(oil-1,x,y+1),g(oil,x,y),0,0);
					}
					if(x-1>0){
						add(g(oil,x,y),g(oil-1,x-1,y),1,b);
						add(g(oil-1,x-1,y),g(oil,x,y),0,-b);
					}
					if(y-1>0){
						add(g(oil,x,y),g(oil-1,x,y-1),1,b);
						add(g(oil-1,x,y-1),g(oil,x,y),0,-b);
					}
				}
			}
		}
	}
	zkw();
	write(ans);
}

P4015

留坑

P2770

留坑

P2754

留坑

P2762

留坑

P3254

Link

感觉也挺裸的最大流

自我感觉网络流难就难在建图上。就以样例为例，先上图（中间的边有点乱，懂就行了），\(1\)_{$4$为单位,$5$}\(9\)为圆桌

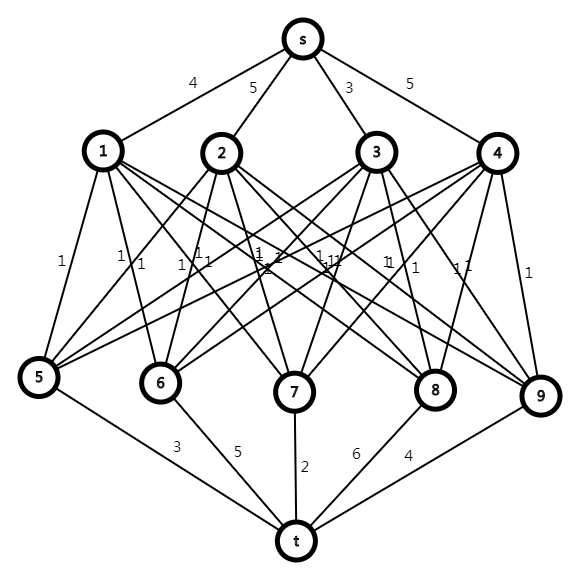
因为每个单位的人都可以去每一个桌，唯一的限制就是每个单位每个桌只能去\(1\)个人，所以不难想到把每个单位和每个圆桌都连上边，然后边的最大容量为\(1\)，这样就限制了只能去一个人的条件。因为每个单位只有一定的人数，所以将源点\(s\)连至每个单位，最大容量为\(r_i\)，这样也就限制了每个单位的人数。同理，将每个圆桌与汇点\(t\)连边，边的容量为\(c_i\)，这样也保证了每个圆桌不会超过限坐人数。于是图建好了。

回到题目，题目要求我们求出有没有方案满足条件要求，于是跑一遍最大流判断最终到\(t\)的流是否大于\(0\)就行了。如果满足，那么遍历一遍每个单位，看看与哪个圆桌连的边（从上到下）中有流再输出它就是答案了。注意，如果有哪个单位的人没有坐上圆桌，那么也不满足要求，输出\(0\)（我在这里被坑了好久……）

代码：

#include<bits/stdc++.h>
using namespace std;
using namespace my_std;
ll m,n,s,t,r[303],head[1000001],cnt=1,dep[1000001],ans=0;
bl ck;
struct node{
	ll nxt,to,w;
}e[1000001];
void add(ll u,ll v,ll w){
	e[++cnt].nxt=head[u];
	e[cnt].to=v;
	e[cnt].w=w;
	head[u]=cnt;
}
bl bfs(){
	memset(dep,0,sizeof(dep));
	queue<ll> q;
	q.push(s);
	dep[s]=1;
	while(!q.empty()){
		ll u=q.front();
		q.pop();
		go(u){
			ll v=e[i].to;
			if(e[i].w&&!dep[v]){
				dep[v]=dep[u]+1;
				q.push(v);
			} 
		}
	}
	return dep[t];
}
ll dfs(ll u,ll flow){
	if(u==t||(!flow)) return flow;
	ll k,res=0;
	go(u){
		ll v=e[i].to;
		if(e[i].w&&dep[v]==dep[u]+1){
			k=dfs(v,min(flow,e[i].w));
			if(!k) dep[v]=maxinf;
			e[i].w-=k;
			e[i^1].w+=k;
			res+=k;
			flow-=k;
		}
	}
	return res;
}
int main(){
	m=read(),n=read();
	s=0;
	t=m+n+1;
	fr(i,1,m){
		r[i]=read();
		add(s,i,r[i]);
		add(i,s,0);
	}
	fr(i,m+1,m+n){
		ll c=read();
		fr(j,1,m){
			add(j,i,1);
			add(i,j,0);
		}
		add(i,t,c);
		add(t,i,0);
	}
	while(bfs()) ans+=dfs(s,maxinf);
	ck=chs(ans,0,1);
	fr(u,1,m){
		ll tot=0;
		go(u){
			ll v=e[i].to;
			if(v!=s&&e[i^1].w) tot++;
		}
		if(tot!=r[u]) ck=1;
	}
	if(ck){
		write(0);
		return 0;
	}
	writeln(1);
	fr(u,1,m){
		ll tot=0;
		go(u){
			ll v=e[i].to;
			if(v!=s&&e[i^1].w) writesp(v-m);
		}
		enter;
	}
}

P4012

留坑

P1251

留坑

P2763

留坑

P2766

留坑

P3355

留坑

P3357

留坑

P4013

留坑

P2765

留坑

P3356

留坑

P2764

留坑

P2775

留坑