【学习笔记】wqs二分

参考博客+图源：wqs 二分学习笔记 - 知乎 (zhihu.com)，侵删

大概是我自己的一些理解

先从这道题入手188. 买卖股票的最佳时机 IV - 力扣（LeetCode） (leetcode-cn.com)

它要求我们求出 交易数\(\leq k\)时的最大收益

一、首先我们考虑恰好交易\(k\)次的最大收益

设\(g_k=\)交易数为\(k\)时的最大收益

我们可以发现\(g_{k+1}-g_k\leq g_k-g_{k-1}\)

也就是后面的交易带来的新的收益一定低于之前的交易带来的收益

怎么证明？

考虑反证法：若后面的交易收益更大，我们可以将前后的两个交易交换，这样\(g_k\)会更优

由这个性质，我们可以画出\(k-g(k)\)的图像（注意这里不是减号，是二维坐标系）

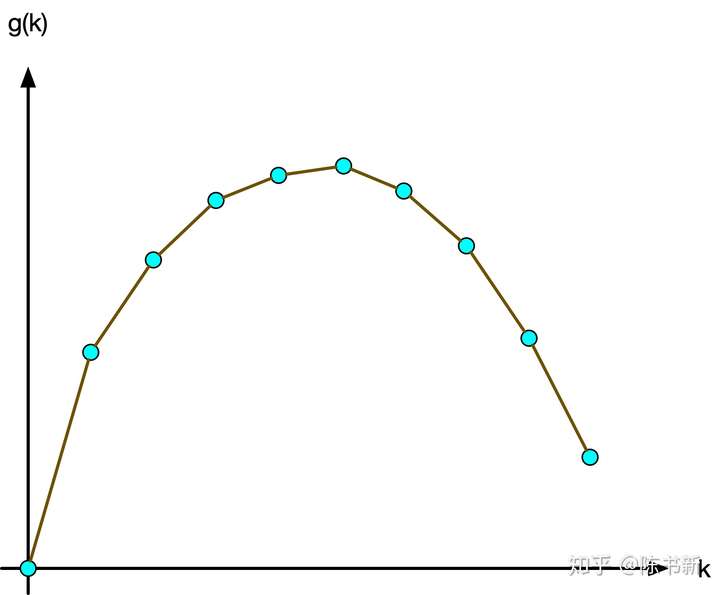
注意到这是一个上凸壳

考虑拿一条直线来切这个上凸壳，它长成这样：

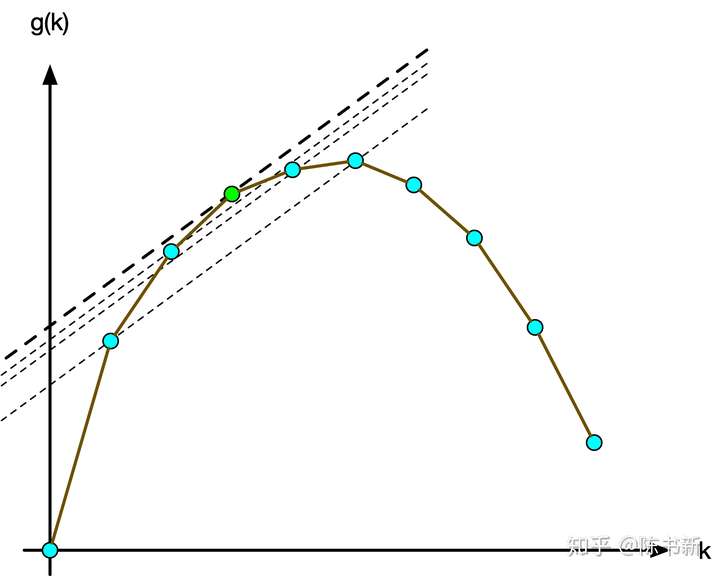
设斜率为\(c\)

那么这条直线在\(y\)轴上的截距为\(g(k)-kc\)

已知这个截距和\(c\)时我们就可以求出\(g(k)\)了

我们会想一下\(k\)的定义：交易的次数

那么这个截距的意义即为：每次交易需要花费\(c\)的手续费，不限次数后得到的最大收益

对于这个问题，我们可以看714. 买卖股票的最佳时机含手续费 - 力扣（LeetCode） (leetcode-cn.com)

它是可以在\(O(n)\)时间内解决的，同时可以求出最优的\(k\)

具体怎么做可以看题解

由于\(c\)越大，对应的\(k\)一定会越小（上凸壳性质）

所以我们考虑二分\(c\)，当得到的\(k=K\)（\(K\)为我们要求的交易次数）时，我们就可以通过\(c\)和当前的截距求出\(g(k)\)

二、考虑把恰好为\(k\)次操作拓展为最多\(k\)次操作

分为两种情况

1.\(k\)在上凸壳的左半部分，即\(g(k)\)单调递增的部分

​ 容易发现恰好交易\(k\)次一定是最优的，且一定能找到答案

2.\(k\)在上凸壳的右半部分，即\(g(k)\)单调递减的部分

​ 二分查找找不到答案，此时答案即为选取任意次的答案，直接做即可

注意：

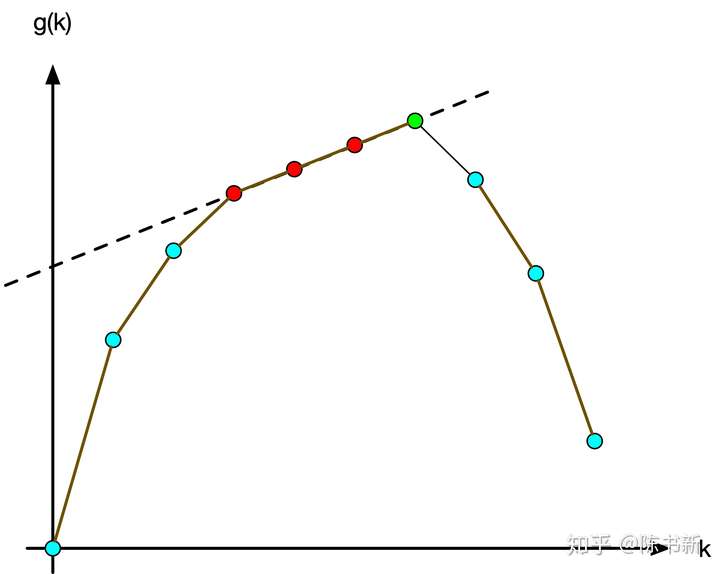
当存在一些点答案相同时，选取\(k\)最大的点，如图中的绿点

实现上我们只需要把操作\(\geq k\)的点全部加入，然后取与\(k\)最近的点即可

三、关于二分的一些问题

1.上下界

本题中：

\(r\)显然可以无限大，依据具体题面而定

\(l\)我认为可以从0开始，但是原博客说要设为1，不是太懂

其他题目具体而定，有时候斜率的值可以有正有负

2.二分值

二分的值是整数，为什么？

因为相邻两个点之间的斜率为\(\dfrac{g_k-g_{k-1}}{k-(k-1)}=g_k-g_{k-1}\)为整数

然后呢？做完了！

update：我也不知道为什么，但是对一些东西排序的时候cmp函数一定得写好，不然有可能RE！