[线段树][dp] Codeforces 1609E William The Oblivious

题目大意

给定一个长为 \(n(n\leq 10^5)\) 的只含有字符 abc 的字符串 \(s\)，\(q(q\leq 10^5)\) 次询问，每次询问给出 \(p,x(x\in\{a,b,c\})\)，将 \(s[p]\) 修改为 \(x\)，然后计算此时使得整个字符串中不含有子序列abc的最小代价（你可以花费1点代价修改任意一个位置上的字符，可以修改任意次）。

题解

考虑在字符串中去匹配子序列abc的过程，可以构造出以下自动机：

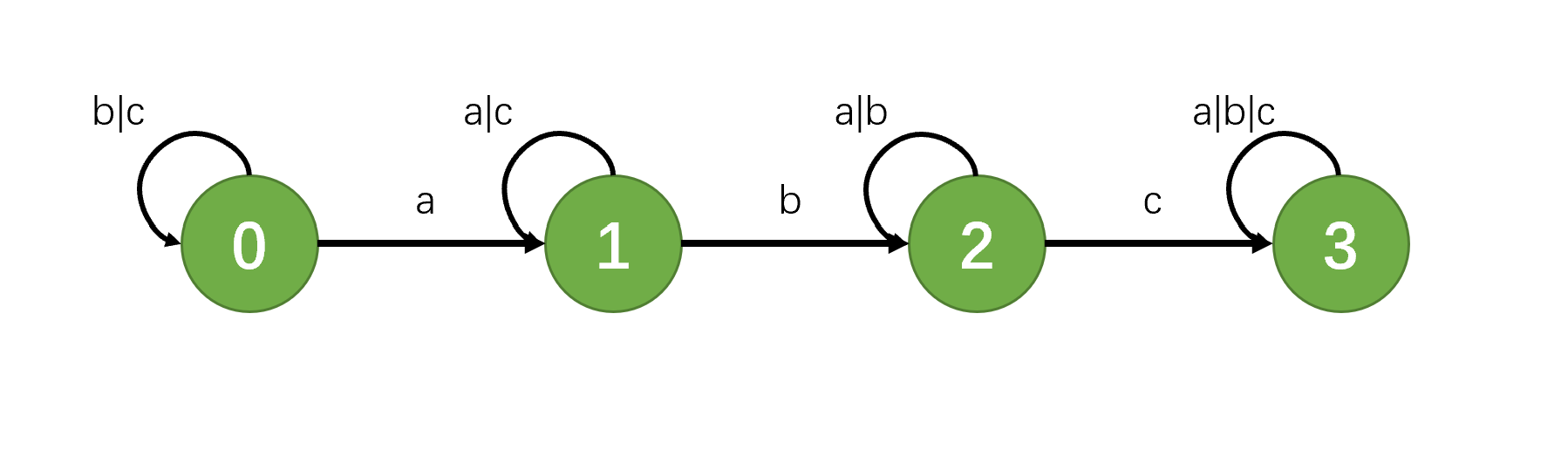
那么可以用线段树来解决，线段树上的每个结点维护 \(s[L:R]\) 这个子串，从自动机的 \(i\) 号点开始匹配，最终走到自动机的 \(j\) 号点的最小代价。转移就是 \(dp[rt][i][j]=min(dp[lson][i][k]+dp[rson][k][j])\)。子序列的匹配问题不妨构建出自动机，可以更明确状态。

Code

#include <bits/stdc++.h>
using namespace std;

struct SegmentTree {
    int T[400010][4][4];
    char s[100010];

    void push_up(int rt) {
        for (int i = 0; i < 4; ++i) {
            for (int j = i; j < 4; ++j) {
                int temp = 0x3f3f3f3f;
                for (int k = i; k <= j; ++k)
                    temp = min(temp, T[rt << 1][i][k] + T[rt << 1 | 1][k][j]);
                T[rt][i][j] = temp;
            }
        }
    }

    void calc(int rt, int p) {
        if (s[p] == 'a') {
            T[rt][0][0] = 1;
            T[rt][1][1] = T[rt][2][2] = T[rt][3][3] = 0;
            T[rt][0][1] = 0;
            T[rt][1][2] = T[rt][2][3] = 1;
        }
        else if (s[p] == 'b') {
            T[rt][1][1] = 1;
            T[rt][0][0] = T[rt][2][2] = T[rt][3][3] = 0;
            T[rt][1][2] = 0;
            T[rt][0][1] = T[rt][2][3] = 1;
        }
        else if (s[p] == 'c') {
            T[rt][2][2] = 1;
            T[rt][0][0] = T[rt][1][1] = T[rt][3][3] = 0;
            T[rt][2][3] = 0;
            T[rt][0][1] = T[rt][1][2] = 1;
        }
    }

    void Build(int rt, int L, int R) {
        if (L == R) { calc(rt, L); return; }
        int mid = (L + R) >> 1;
        Build(rt << 1, L, mid);
        Build(rt << 1 | 1, mid + 1, R);
        push_up(rt);
    }

    void Update(int rt, int L, int R, int pos, char c) {
        if (L == R) { s[L] = c; calc(rt, L); return; }
        int mid = (L + R) >> 1;
        if (pos <= mid) Update(rt << 1, L, mid, pos, c);
        else Update(rt << 1 | 1, mid + 1, R, pos, c);
        push_up(rt);
    }
};
SegmentTree Tree;
int n, q;

int main() {
    scanf("%d%d", &n, &q);
    scanf("%s", Tree.s + 1);
    Tree.Build(1, 1, n);
    while (q--) {
        int p; char c;
        scanf("%d", &p); getchar();
        scanf("%c", &c); getchar();
        Tree.Update(1, 1, n, p, c);
        printf("%d\n", min(Tree.T[1][0][0], min(Tree.T[1][0][1], Tree.T[1][0][2])));
    }

    return 0;
}