[计算几何][圆反演] 2019 ICPC区域赛沈阳站E.Capture Stars

题目大意

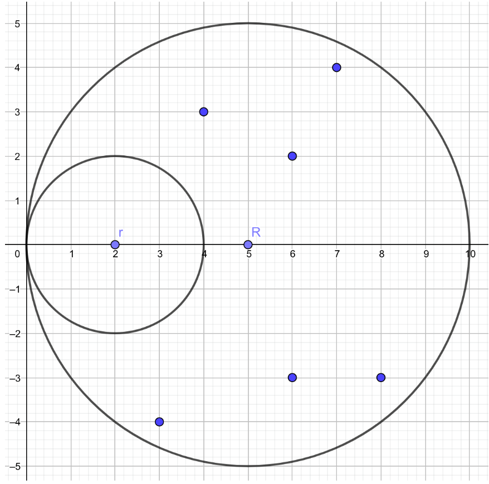
题目求与两圆相切的虚线圆最多能覆盖多少给定点。
大圆小圆圆心均在正向x轴上且内切在坐标轴原点，因此大圆圆心\((R,0)\),小圆圆心\((r,0)\)。

题解

Code

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
using namespace std;

#define RG register int
#define LL long long

const double eps = 1e-8;

int sgn(double x){
    if(fabs(x)<eps)return 0;
    if(x<0)return -1;
    else return 1;
}

inline double sqr(double x){return x*x;}

struct Point{double x,y;};
struct Node{int Value;double y;};
Point Data[10010];
vector<Node> Sum;
int T,N;LL R,r;

bool cmp(Node A,Node B){
    if(sgn(A.y-B.y)==0) return A.Value>B.Value;
    return A.y<B.y;
}

int main(){
    scanf("%d",&T);
    while(T--){
        Sum.clear();
        scanf("%d%lld%lld",&N,&R,&r);
        double mid=(double)R+(double)(R*R)/(double)r;
        double rr=(double)(R*R)/(double)r-(double)R;
        for(RG i=1;i<=N;++i){
            LL x,y;scanf("%lld%lld",&x,&y);
            Data[i].x=(double)(4LL*R*R*x)/(double)(x*x+y*y);
            Data[i].y=(double)(4LL*R*R*y)/(double)(x*x+y*y);
            //点的反演
            if(sgn(fabs(Data[i].x-mid)-rr)==0){
                Sum.push_back((Node){1,Data[i].y});
                Sum.push_back((Node){-1,Data[i].y});
            }
            else if(sgn(fabs(Data[i].x-mid)-rr)<0){
                double h=sqrt(sqr(rr)-sqr(Data[i].x-mid));
                Sum.push_back((Node){-1,Data[i].y+h});
                Sum.push_back((Node){1,Data[i].y-h});
            }
            else continue;
        }
        int Ans=0;
        sort(Sum.begin(),Sum.end(),cmp);
        int Len=Sum.size();
        int temp=0;
        for(RG i=0;i<Len;++i){
            temp+=Sum[i].Value;
            Ans=max(Ans,temp);
        }
        printf("%d\n",Ans);
    }
    return 0;
}