Codeforces 1294E Obtain a Permutation

题目大意

给定一个\(N\times M\) 的矩阵 \((1 \leq N,M \leq 2 \times 10^5 , N \times M \leq 2 \times 10^5)\)，

有两种操作，
操作一：选取任意一个元素，将它改变成任意值
操作二：选取某一列，将这一列的所有元素循环上移一格，如下图将第一列循环上移一格

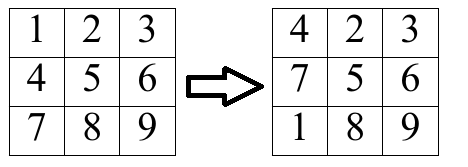
要求用最少的操作步数，使得矩阵变成如下形式

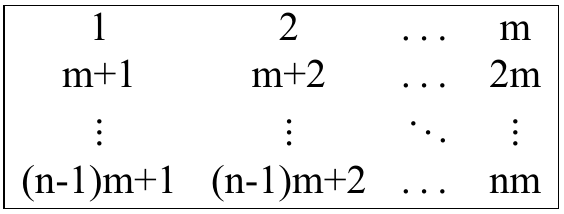
输出最少的操作步数。

题解

我们用输入的矩阵减去最终的矩阵，可以得到一个增量矩阵，对应着原矩阵的每个元素还要变化多少，才能得到最终的矩阵。

容易发现，列与列之间互不干扰，每一列都可以独立计算出这一列的最少操作步数，所有列的最少操作步数相加后即得答案。

举个例子
不妨令\(N=4,M=3\),
则第一列一定是\(1,4,7,10\)
依次使用操作二，
\(1,4,7,10\) 移动0次
\(10,1,4,7\) 移动1次
\(7,10,1,4\) 移动2次
\(4,7,10,1\) 移动3次

每一列的增量矩阵依次变为
\(0,0,0,0\)
\(9,-3,-3,-3\)
\(6,6,-6,-6\)
\(3,3,3,-9\)
可以发现，增量矩阵中的每个元素一定是\(M\)的倍数，否则不符合要求，只能通过操作一去修改

把增量矩阵的每一个元素除以\(M\),得
\(0,0,0,0\)
\(3,-1,-1,-1\)
\(2,2,-2,-2\)
\(1,1,1,-3\)
得到的这个东西很有规律。

可以发现，如果我们把当前列的第\(i\)个元素移动到第一个位置上，需要移动\(i\)次，且这一列的增量矩阵除以\(M\)后只能有上面给出的两个数。

比如\(2,2,-2,-2\)，需要移动\(2\)次，且前\(2\)个元素只能是\(2\)，后两个元素只能是\(-2\)

再比如\(1,1,1,-3\) ，需要移动\(3\)次，且前\(3\)个元素只能是\(1\)，后两个元素只能是\(-3\)

只要维护一个Cnt数组，对于每一列扫一遍它的增量矩阵，即可算出至少需要通过操作一改变几个元素才能再使用\(i\)次操作二得到最终的矩阵。

时间复杂度\(O(MN)\)

Code

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <vector>
using namespace std;

vector<int> Data[200010];
int Cnt[400010];
int N,M;

template<typename elemType>
inline void Read(elemType &T){
    elemType X=0,w=0; char ch=0;
    while(!isdigit(ch)) {w|=ch=='-';ch=getchar();}
    while(isdigit(ch)) X=(X<<3)+(X<<1)+(ch^48),ch=getchar();
    T=(w?-X:X);
}

inline int Calc(int pos){
    for(register int i=0;i<N;++i){
        int x=Data[pos][i];
        if(x%M!=0) continue;
        x/=M;
        if(x>N-1 || x<-(N-1)) continue;
        if(x<=0 && i>=-x) ++Cnt[x+N-1];
        else if(x>0 && i<N-x) ++Cnt[x+N-1];
    }
    int Res=2147483647;
    for(register int i=0;i<=N-1;++i){
        int temp=(N-i)-Cnt[N-i-1]+i-Cnt[N-i+N-1]+i;
        Res=min(Res,temp);
    }
    for(register int i=0;i<2*N-1;++i)
        Cnt[i]=0;
    return Res;
}

int main(){
    Read(N);Read(M);
    for(register int i=1;i<=N;++i){
        for(register int j=1;j<=M;++j){
            int x;Read(x);
            Data[j].push_back(x-((i-1)*M+j));
        }
    }
    int Ans=0;
    for(register int i=1;i<=M;++i)
        Ans+=Calc(i);
    cout<<Ans<<endl;

    return 0;
}