Datawhale 吃瓜教程 Task05打卡

支持向量机

从几何角度，对于线性可分数据集，支持向量机就是找距离正负样本都最远的超平面，相比于感知机，

其解是唯一的。

如果数据是分布在一个二维平面上的，那么我们可以找到一条直线将正负样本分开。

对于多维空间，我们可以找到n-1维度的平面将正负样本分开。

在样本空间中，划分超平面可通过如下线性方程描述

\[w^Tx+b=0 \]

其中\(w=(w_1;w_2;...;w_d)\)为法向量，决定了超平面的方向；b为位移项决定了超平面与原点之间的距离，显然超平面是由\(w\)与\(b\)决定的。

样本空间中任意点\(x\)到超平面的距离为

\[r=\frac{|w^Tx+b|}{||w||} \]

当\(y_i=+1\)时有

\[w^Tx_i+b\geq+1 \]

当\(y_i=-1\)时有

\[w^Tx_i+b\leq+1 \]

左右两边同乘以y有

\[y(w^Tx+b)\geq1 \]

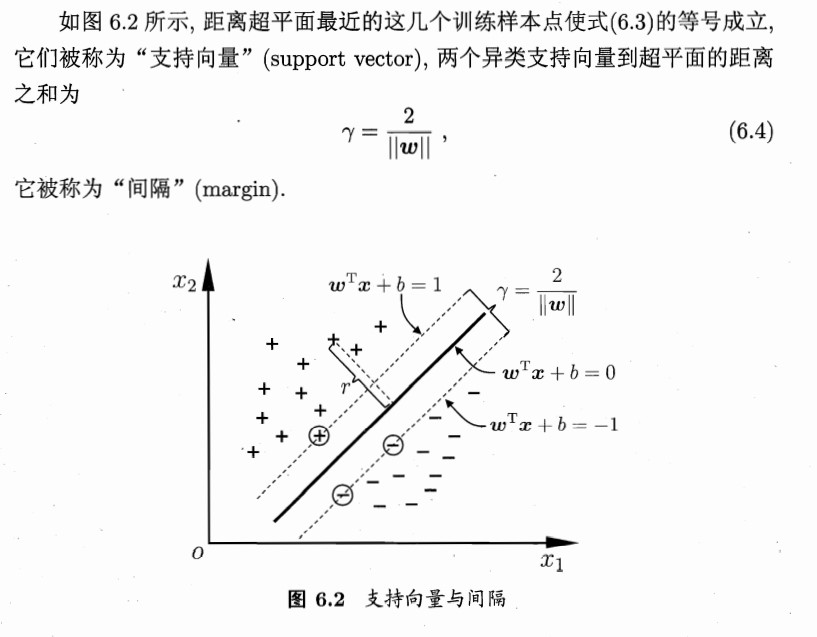
根据前面支持向量到超平面的距离公式，两个异类支持向量到超平面的距离为

\[max2* {\frac{y(w^Tx+b)}{||w||}} \]

则有\(\gamma=\frac{2}{||w||}\)

最大化间距等同于最小化间距倒数的平方所以有

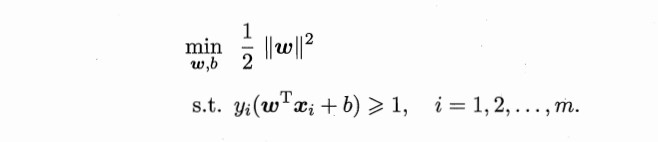
对偶问题

上述式子其实本身是一个凸二次规划问题，使用拉格朗日乘子法可得到其对偶问题

将支持向量机原问题转化为拉格朗日对偶问题求解主要有如下两个原因：

• 无论原问题是否为凸优化问题，对偶问题恒为凸优化问题，因为对偶函数恒为凹函数（加负号即可转化为凸函数）。而且原始问题的时间复杂度与特征维数成正比（若特征维数大，会导致出现维数灾难问题），而对偶问题和数据量成正比，当特征维数远高于数据量的时候，采用拉格朗日对偶问题求解更高效
• 对偶问题能引入核函数，进而可推广到非线性分类问题

核函数

线性分类器无法用于求解线性不可分的情况

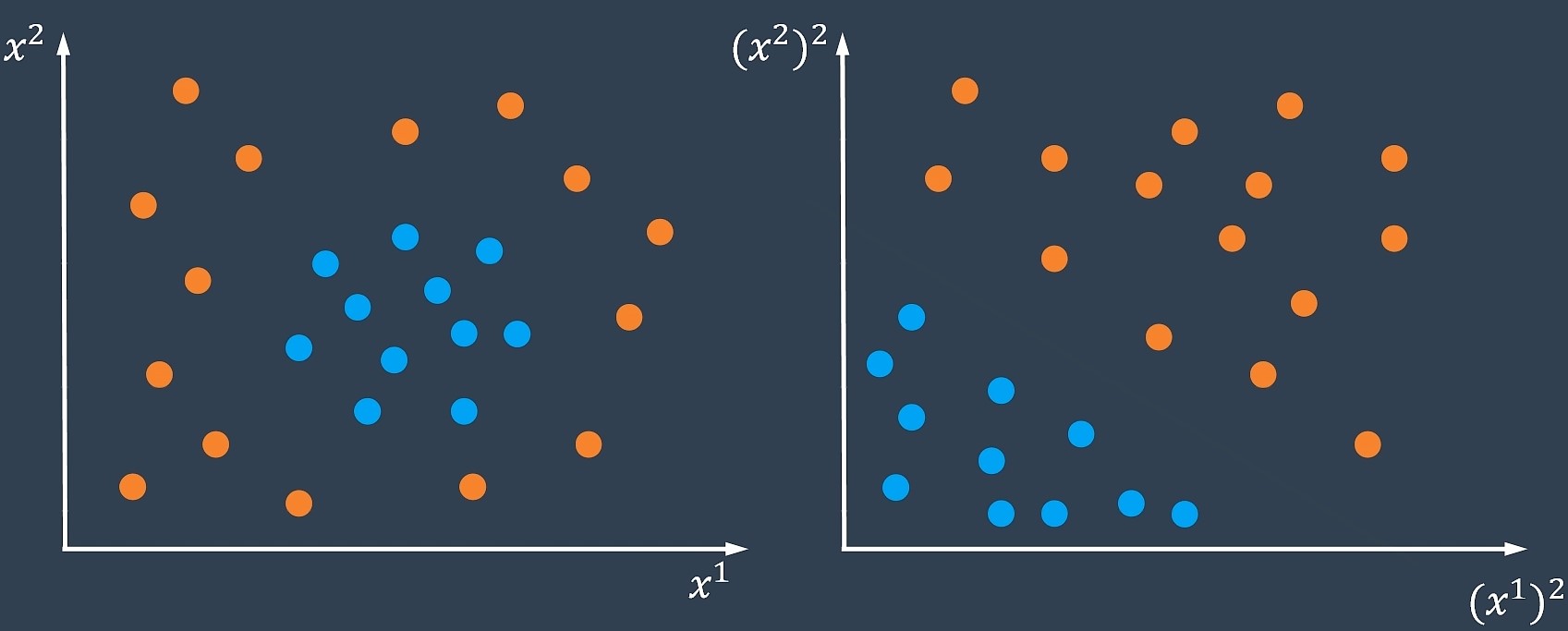
对于这种情况可以选择将原样本空间映射到一个更高维的特征空间中。

核函数可以直接计算隐式映射到高维特征空间后的向量内积，而不需要显式地写出映射后的结果，它虽然完成了将特征从低维到高维的转换，但最终却是在低维空间中完成向量内积计算，与高维特征空间中的计算等效（低维计算，高维表现），从而避免了直接在高维空间无法计算的问题。引入核函数后，原来的对偶问题变为：

同时确定核函数存在已经选择核函数可采用以下定理

软间隔与正则化

在现实任务中，线性不可分的情形才是最常见的。因此我们允许部分样本不满足之前的约束条件，也就是软间隔。

由上式可知，当满足约束条件时，损失为0；不满足约束条件时，损失不为0。
当C取\(+ ∞\)时，为最小化目标函数式(6.29)，会迫使所有样本满足上述约束条件，进而导致所有样本的损失为0，使得软间隔问题退化为硬间隔问题。当C取有限值时，则允许一些样本不满足约束条件。

支持向量回归

直观来说，它的约束条件是让模型寻找出一个条状区域而不是一条直线。