Datawhale 吃瓜教程 Task03打卡

ID3决策树

自信息

\[I(x)=-log_bp(x) \]

可以先把自信息理解成跟米，公顷一样的一种单位，不必在这纠结

信息熵

度量随机变量 \(X\)的不确定性，信息熵越大越不确定

\[H(x) = E[I(X)] = -\sum_xp(x)log_bp(x)\tag{以离散型为例} \]

在计算时约定 如果 p(x) = 0 ，则 \(p(x)log_bp(x)=0\)

假设随机变量\(X\)有三个可能的取值\(a,b,c\)，那么三者满足\(p(a)+p(b)+p(c)=1\)

现在请根据直观感受回答下面的两个问题：

1: 啥时候信息熵最小呢？（信息熵越大越不确定）

当然是 \(a,b,c\) 中某个的取值为1的时候，比如说如果 \(p(a)=1\)，那么 \(X\) 的取值恒等于 a ，也不用猜了，相当于一个常量。常量当然是确定性的，所以这时候X的信息熵为0。

2: 那什么时候信息熵最大呢？（也就是最不确定 \(X\) 的取值的情况）

当 \(X\) 的各个取值概率均等时，信息熵最大，值为 \(lob_b|X|\) ，其中\(|X|\) 表示 \(X\) 可能取值的个数。猜哪个的概率都一样，只能瞎蒙了，这时候不确定性是最高的。

比如电视答题里面有题目让你选对错，但你完全不知道题目的相关背景，这时候选 √，× 对你来说完全一样，50%，50%。但如果这时候使用一次去除错误选项的机会，这样你就只有一个选项可以选了，并且选这个肯定对，那 \(X\)又变为常量了，信息熵重新变为0。

将样本类别标记\(y\)视作随机变量，将各个类别在样本中的占比 \(p_k(k=1,2...|\gamma|)\) 视作各个类别取值的概率，则样本集合 \(D\) 的信息熵为(对数b取2):

\[Ent(D) = - \sum_{k=1}^{|\gamma|}p_klog_2p_k \]

这里的 \(Ent(D)\) 其实就是之前的 \(H(X)\)，然后书中说的\(Ent(D)\)越小，纯度越高其实就是信息熵越小，样本可能的取值越确定的意思。

西瓜数据集

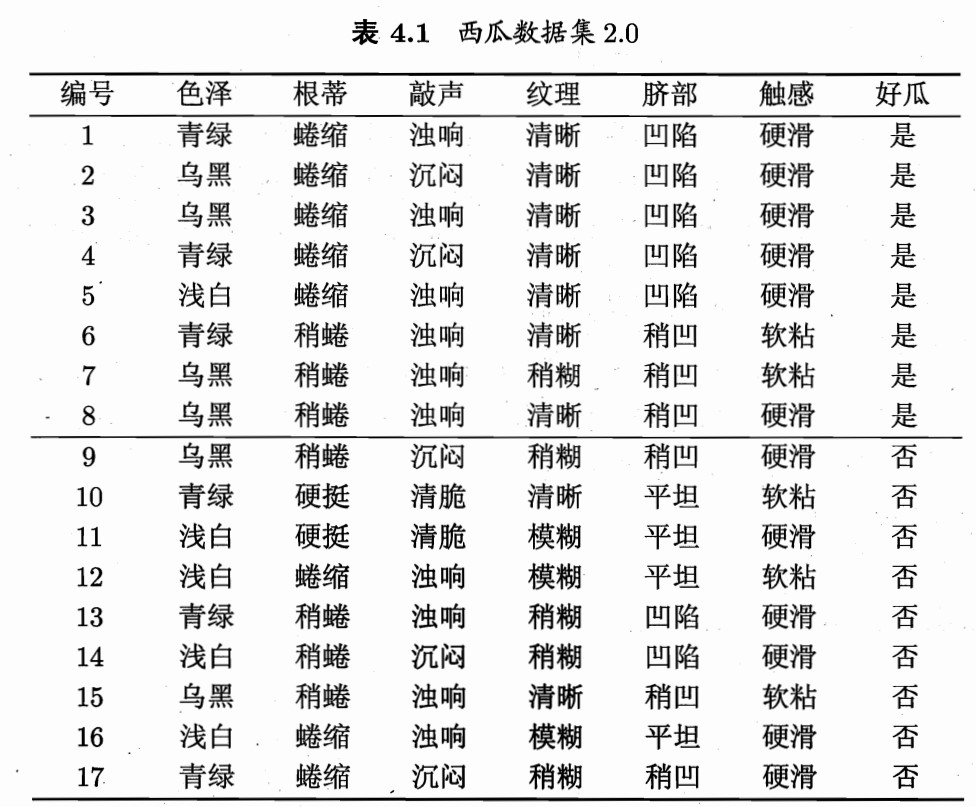
以西瓜数据集为例，一颗判断是否为好瓜的决策树显然 \(|\gamma|\)为2（是好瓜，不是好瓜），在这17个样例中好瓜的个数为8，坏瓜9个。也就是正例 \(p_1=\frac{8}{17}\) ，反例 \(p_2=\frac{9}{17}\)

那么

\[\begin{split} Ent(D) &= -\sum_{k=1}^{2}p_klog2p_k \\ &= -(\frac{8}{17}log_2\frac{8}{17}+\frac{9}{17}log_2\frac{9}{17}) \\ &=0.998 \end{split} \]

条件熵

条件熵是指 \(Y\) 的信息熵关于概率分布 \(X\)的期望

\[H(Y|X) = \sum_xp(x)H(Y|X=x) \]

从单个特征 \(\alpha\) 的角度来说，假设其可能取值为 \({a^1,a^2,..a^v}\) ，\(D^v\) 表示属性$ \alpha $取值为 \(\alpha^v \in \{{a^1,a^2,..a^v}\}\)的样本集合，\(\frac{|D^v|}{|D|}\)表示占比，则在知道 α 的取值之后，\(D\) 的条件熵为:

\[\sum_{v=1}^V\frac{{D^v}}{D}Ent(D^v) \]

信息增益

而信息增益其实就是值在某个属性的取值已知后，随机变量的不确定性减小的程度

\[Gain(D,a) =Ent(D) -\sum_{v=1}^V\frac{{D^v}}{D}Ent(D^v) \]

假设我们知道了西瓜数据集中关于色泽的概率分布

\[Ent(D^{色泽=青绿}) = -(\frac{3}{6}log_2\frac{3}{6}+\frac{3}{6}log_2\frac{3}{6}) = 1.000 \\ Ent(D^{色泽=乌黑}) = -(\frac{4}{6}log_2\frac{4}{6}+\frac{2}{6}log_2\frac{2}{6}) = 0.918\\ Ent(D^{色泽=浅白}) = -(\frac{1}{5}log_2\frac{1}{5}+\frac{4}{5}log_2\frac{4}{5}) = 0.722 \]

那么知道了属性“色泽”的信息增益为

\[\begin{split} Gain(D,色泽) &= Ent(D) - \sum_{v=1}^3\frac{{|D^v|}}{|D|}Ent(D^v) \\ &= 0.998 - (\frac{6}{17}*1.000 + \frac{6}{17}*0.918 + \frac{5}{17}*0.722) \\ &= 0.109 \end{split} \]

结果为正，说明知道确定色泽信息之后有助于我们判断西瓜的好坏。

C4.5决策树

如果计算“编号”这一属性的信息增益，你会发现它直接等于0.998，因为每个编号对应的西瓜的情况是确定的。\(Ent(D)\) 为 0

但很显然这种提升是没有用的，信息增益会对这种能够划分特别多值，并且每个取值下数目较少的属性产生偏好，比如之前说的 “编号” 这一属性。

增益率

增益率能够减少可能取值较多的属性偏好带来的不利影响。

\[Gain\_ratio(D,a) = \frac{Gain(D,a)}{IV(a)}\\ IV(a) = -\sum_{v=1}^V\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|} \]

\(a\)的可能取值个数\(V\)越多，通常\(IV(a)\)也会越大，虽然它解决了ID3的问题。但这个增益率对可能取值数目少的属性会有偏好，因为它们作为分母的\(IV(a)\)比较小。

有一种拆东墙补西墙的感觉。。。

最终方案

C4.5并没有完全使用增益率代替信息增益，而是采用了一种启发式的方法：先选出信息增益高于平均水平的属性，再从中选择增益率最高的。

CART决策树

基尼值

从样本集合 \(D\)中随机抽取两个样本，标记不同概率。因此基尼值越小，碰到异类的概率越小，纯度越高

\[Gini(D) = \sum_{k=1}^{|\gamma|}\sum_{k'\neq{k}}p_kp_{k'} = \sum_{k=1}^{|\gamma|}p_k(1-p_k) = 1 - \sum_{k=1}^{|\gamma|}p^2_k \]

基尼指数

属性\(\alpha\)的基尼指数

\[Gini\_index(D,\alpha) = \sum_{v=1}^V\frac{|D^v|}{D}Gini(D^v) \]

CART决策树：选择基尼指数最小的属性作为最优划分属性

\[a_*=\mathop{argmin}\limits_{a\in{A}} Gini\_index(D,\alpha) \]

具体划分点的选择：

• 对每个属性a的各一个可能取值\(v\)，将数据集\(D\)分为 \(a=v,a\neq v\)两部分计算基尼指数

  \[Gini\_index(D,a) = \frac{|D^{a=v}|}{D}Gini(D^v) + \frac{|D^{a\neq v}|}{D}Gini(D^{a \neq v}) \]

• 然后选择基尼指数最小的属性以及对应取值作为最优划分属性和最优划分点

• 重复以上两步，直至满足停止条件