Datawhale 吃瓜教程 Task02打卡

主要参考了大佬的视频，第三章的公式推导对我这种零基础渣渣来说真是要命

线性回归算法原理

极大似然估计

类似于以偏概全，在极大似然估计中我们选择相信获得的样本数据已经能够很好的概括现实情况中的真实数据分布。将求出的样本数据的概率分布作为我们现实情况中的概率分布使用。

x=1 y=2

x=2 y=4

x=3 y=6

x=4 y=?

如果问你❓处应该填几，相信你一定会猜一个8。

例子：通过 发际线高度 预测 计算机水平

线性回归求的不是点到直线的垂直距离（正交回归求的是点到直线的距离），而是实际值 y 与预测值y' 之间的差值，也就是预测误差。线性回归最后要找的点就是均方误差最小的那条直线

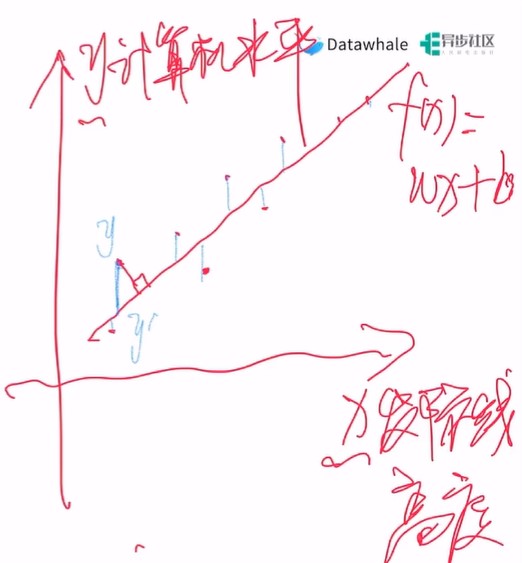
咱们当然可以仅仅通过发际线高度来预测计算机水平，但一般情况下的模型通常有多个变量

毫无疑问不管有多少个特征，我们最后都需要求出来f(x) 中的 w 与 b

求解w和b

最小二乘法

最小二乘法做的事情就是将均方误差最小化即

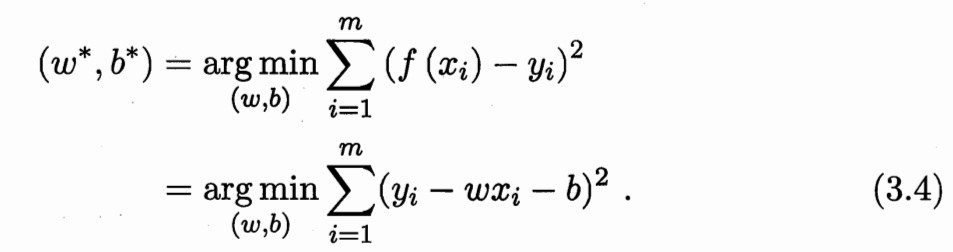
上述（3.4）值最小，具体的w,b求解公式相信大家高中数学课上都见过，现在我们来看看课本上的式子是如何推导出来的。

凸集

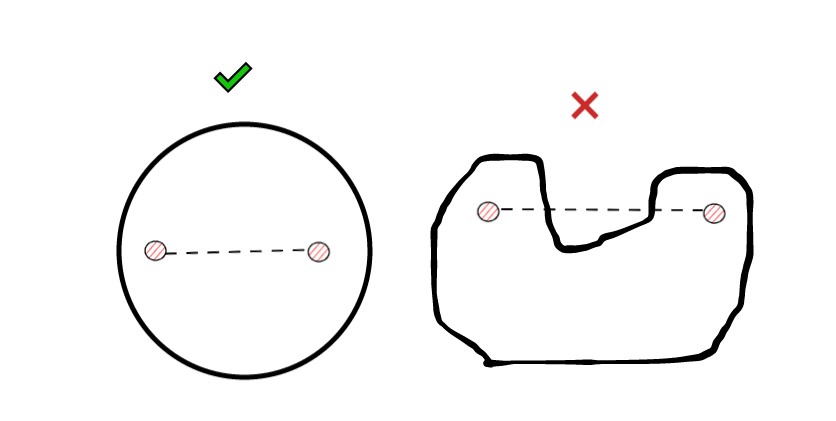
凸集：若两个点属于此集合，则这两点连线上的任意一点均属于此集合。换句话说如果连线上有任意一点不属于该集合，则这个集合不能被叫做凸集。

多元函数求解

多元函数的一阶导数（梯度）

为啥是列向量大佬在视频里面好像也没有怎么提，只是说是习惯问题。求梯度就是求偏导，将各个变量的偏导求出来之后拼成一个列向量就好了。

多元函数的二阶导数

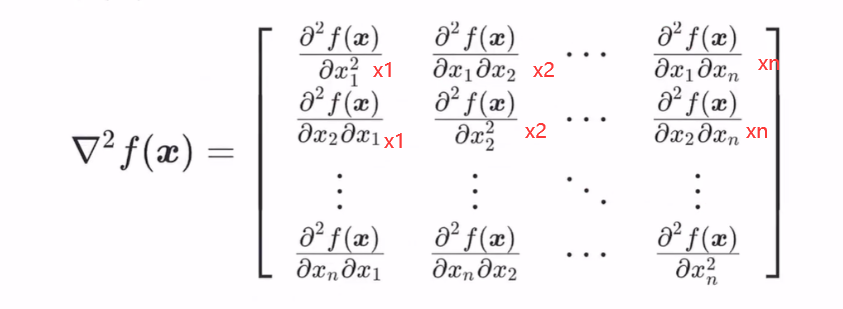
二阶偏导数就是老老实实的在原来一阶导数的基础上对各变量进行求偏导即可。

根据这个定理，我们首先求（w,b）的海塞矩阵（二阶导），求得的矩阵如下图。

然后只要证明出该矩阵是半正定的即可。

顺序主子式通俗的来说就是取原始的前m行m列(n=1.2..n)，就是行列顺序增大直到跟原大小一样，这些矩阵就叫顺序主子式

所以这里一共有两个顺序主子式，分别是 [1 * 1] 和 [2 * 2]

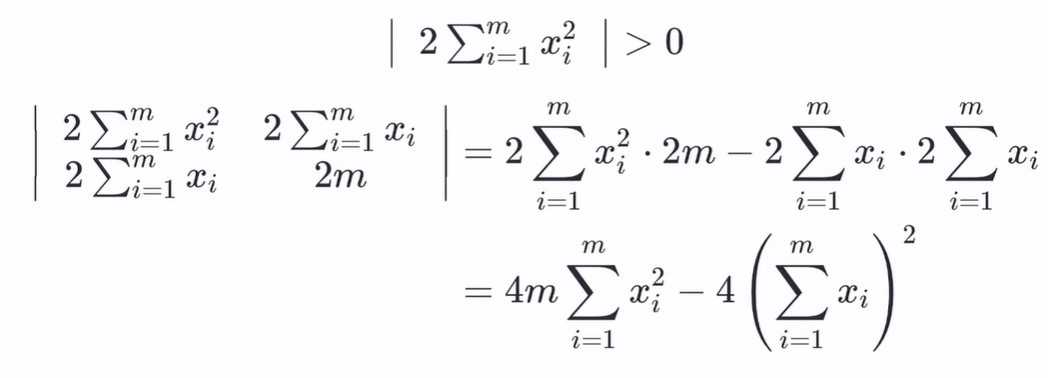
第一个是x的平方求和肯定大于0，然后第二个主子式交叉相乘再相减得到的结果如上图。现在就是要看第二个顺序主子式是否大于0。

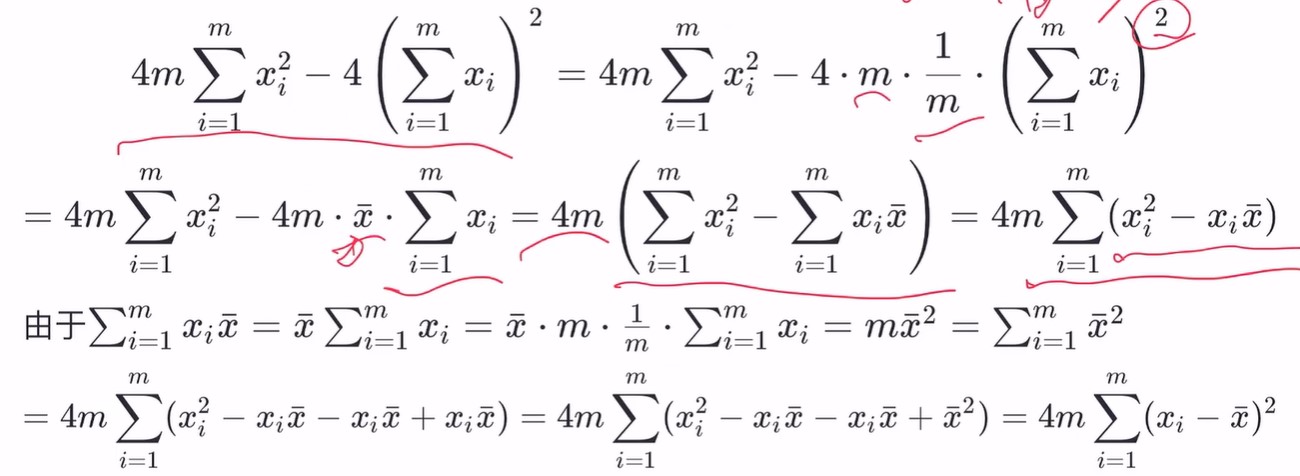
所有顺序主子式非负，所以该矩阵为半正定矩阵。根据前面的定理可得 E(w,b)是关于 w,b的凸函数。

证明了它是凸函数就好办了，因为凸函数有个性质：

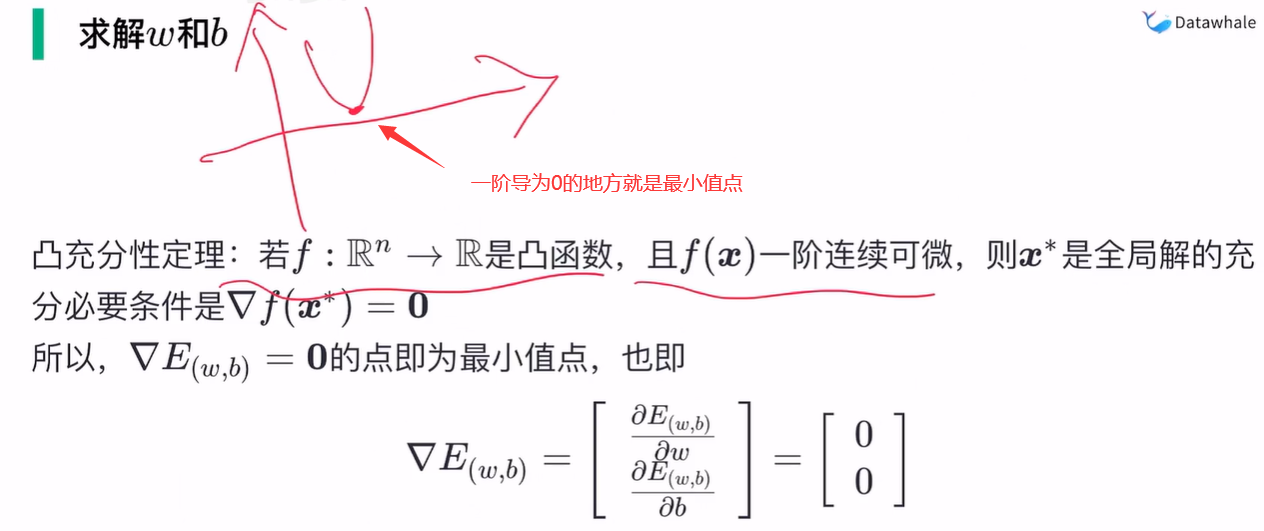
对 w 和 b 分别求导

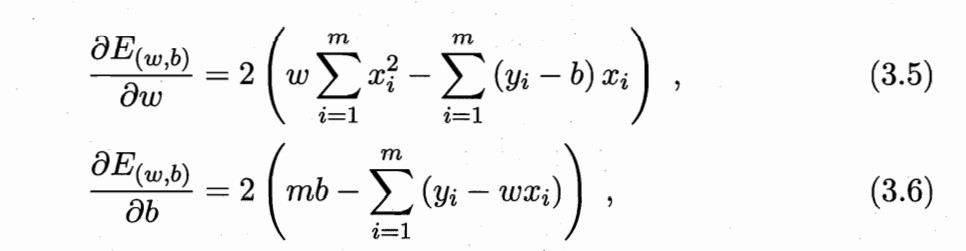
然后令上述两式分别为零，求得的最终结果就是咱们高中课本里面的式子了

多元线性回归

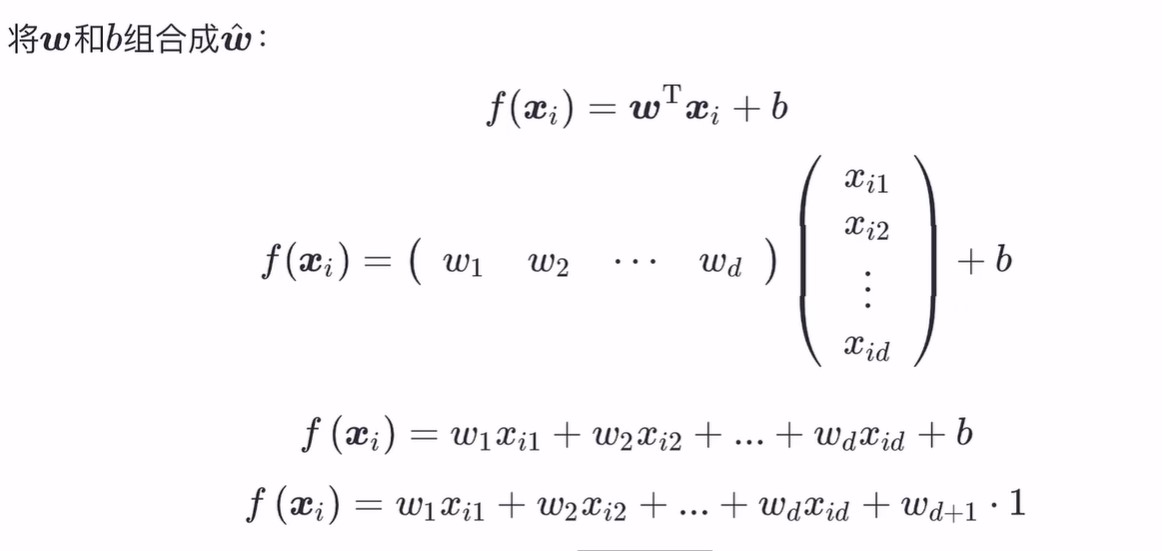
多元问题下我们可以统一一下函数形式，将 b 用 W(d+1)*1 的形式来代替，这样整个表达式就能变为

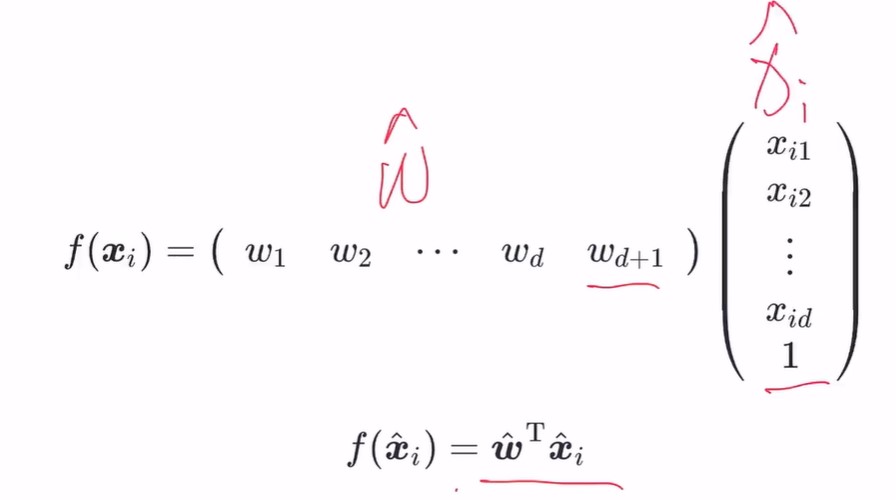
处理非线性问题

当得到的数据散点图是一条近似曲线的时候，没有办法直接套用传统线性回归模型。但其实我们可以通过换元的办法将变量重新"拉"成一条直线。

请看高中数学题😂

很明显题目中第二个模型更符合数据分布，左右取对数，换元得

v = λx+t ，你看现在又变成一元一次函数，变回我们熟悉的线性模型上了。

线性判别分析

给定训练样本，设法将样本投影到一条直线上，使得同类样例的投影点尽可能的接近，异类样例的投影点尽可能的远。
也就是说它想让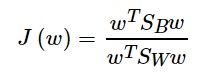
最大

因为分子分母都是关于w的二次项，所以J(w)的最小值与w的长度无关，只与其方向有关。
不妨令

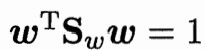
则有


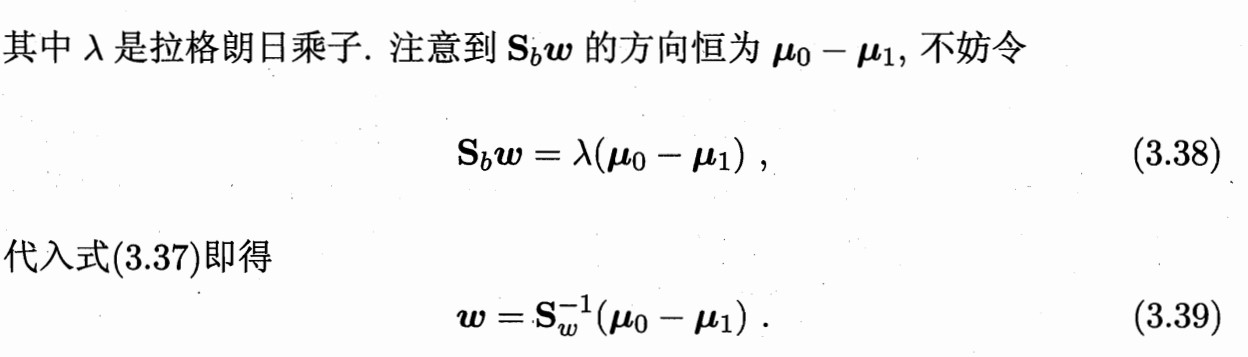
此时求出来的极值点w即为最小值点