Dijkstra笔记
Dijkstra
dijkstra是一个运用了贪心思想和广度优先搜索的单源最短路算法,它的时间复杂度比SPFA的时间复杂度稍低,很适合在没有负边权且不是随机数据(卡SPFA)的情况下使用。
dijkstra运用了贪心的策略,将每个点与起点的距离存到一个dis数组里,若这个点不与起点直接相连则将其的距离看做是无穷大(在这里用\(0x7fffffff\)(int的最大值)代替)。将已经处理好的(确定是最短路的)顶点标记在一个数组里。
那要怎么处理呢?
我们先把与起点直接相连的点遍历一遍,找出与起点距离最小的点,我们在这里称之为A点,把它标记为处理好。为什么这样就把A点处理好了呢?因为按照贪心的思想,A点如果与起点距离最小,那从起点到别的点再到A点的话距离一定会比从起点直接到A点的距离大(这也是为什么dijkstra不适用有负边权的图的原因)。然后我们把所有与A点相连的点全都遍历一遍,如果从起点到A点再到这个点的距离比直接从起点到这个点的距离小的话,那么我们就更新起点到这个点的距离,术语叫做“松弛”。以此类推,一直到所有的顶点都松弛完了为止。
上图开讲
首先我们构造这样一个图
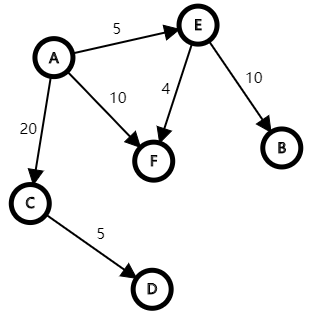
以A为起点,dis数组是这样的(下标从0开始)
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| dis | \(0\) | \(\infty\) | \(20\) | \(\infty\) | \(5\) | \(10\) |
我们遍历一遍dis数组,找出离A最近的点E,并把它标记为已经处理好的点(绿色)。
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| dis | \(0\) | \(\infty\) | \(20\) | \(\infty\) | \(\color{#52C41A}{5}\) | \(10\) |
然后我们遍历与E相连的点,比较从起点到E点再到这个点的距离,如果比从起点直接到这个点的距离短,就更新起点到这个点的距离。如B点,从起点到E点再到B点的距离(15)比从起点直接到B点的距离小(\(\infty\)),于是我们更新dis数组中到B点的距离。(红色表示处理过但不确定,不在程序中标记,只是为了讲着方便)
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| dis | \(0\) | \(\color{Red}{15}\) | \(20\) | \(\infty\) | \(\color{#52C41A}{5}\) | \(10\) |
然后遍历到F点,可得A-B-F的距离(9)小于A-F的距离(10),于是更新dis数组中A-F的距离
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| dis | \(0\) | \(\color{Red}{15}\) | \(20\) | \(\infty\) | \(\color{#52C41A}{5}\) | \(\color{Red}{9}\) |
与E点相连的点遍历完后,我们再次遍历dis数组并找出没有处理过的离A最近的点,重复E点的步骤,直到所有的点都处理完为止。
标记F点为确定的点
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| dis | \(0\) | \(\color{Red}{15}\) | \(20\) | \(\infty\) | \(\color{#52C41A}{5}\) | \(\color{#52C41A}{9}\) |
遍历与F点相连的点并更新距离
没有与F点相连的点,遍历dis数组找下一个
标记B点为确定的点
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| dis | \(0\) | \(\color{#52C41A}{15}\) | \(20\) | \(\infty\) | \(\color{#52C41A}{5}\) | \(\color{#52C41A}{9}\) |
遍历与B点相连的点并更新距离
没有与B点相连的点,遍历dis数组找下一个
标记C为确定的点
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| dis | \(0\) | \(\color{#52C41A}{15}\) | \(\color{#52C41A}{20}\) | \(\infty\) | \(\color{#52C41A}{5}\) | \(\color{#52C41A}{9}\) |
遍历与C点相连的点并更新距离
找到D点,\(20+5<\infty\),更新A点到D点的距离为25
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| dis | \(0\) | \(\color{#52C41A}{15}\) | \(\color{#52C41A}{20}\) | \(\color{Red}{25}\) | \(\color{#52C41A}{5}\) | \(\color{#52C41A}{9}\) |
没有与C点相连的点了,遍历dis数组找下一个
标记D为确定的点
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| dis | \(0\) | \(\color{#52C41A}{15}\) | \(\color{#52C41A}{20}\) | \(\color{#52C41A}{25}\) | \(\color{#52C41A}{5}\) | \(\color{#52C41A}{9}\) |
所有的点都更新完了,我们就得到了A点到所有点的最短路径长度
| 起点 | 终点 | 长度 |
|---|---|---|
| A | A | 0 |
| A | B | 15 |
| A | C | 20 |
| A | D | 25 |
| A | E | 5 |
| A | F | 9 |
这就是利用Dijkstra寻找单源最短路径的方法。
为啥不能用在带负边权的图上呢
那为什么Dijkstra不能用在带有负边权的图上呢?
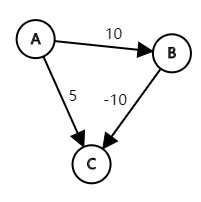
让我们用一个图来解释一下
以A点为起点,最初的dis数组是这样的
| A | B | C | |
|---|---|---|---|
| dis | \(0\) | \(10\) | \(5\) |
如果按照Dijkstra的步骤来,第一步我们会把C点确定
| A | B | C | |
|---|---|---|---|
| dis | \(0\) | \(10\) | \(\color{#52C41A}{5}\) |
然鹅5并不是A点到C点的最短距离,A-B-C的距离是0,这明显比5要小,但是我们已经确定了A-C的距离,我们就不会进行更新,导致输出一个错误的答案
Dijkstra真是个难学的算法
最后是你们最想要的
模板
邻接矩阵存储(起点为1):
void dijkstra()
{
memset(dis,127/3,sizeof(dis));//初始化
v[1]=1;
dis[1]=0;
for(int i=1;i<=n;++i)
{
int k=0;
for(int j=1;j<=n;++j)//找出距离最近的点
if(!v[j]&&(k==0||dis[j]<dis[k]))
k=j;
v[k]=1;//加入集合
for(int j=1;j<=n;++j)//松弛
if(!v[j]&&dis[k]+a[k][j]<dis[j])
dis[j]=dis[k]+a[k][j];
}
}
邻接链表存储(加堆优化):
using namespace std;
const int maxn=250;
struct edge{
int to,dis,next;
//定义边的结构体
};
edge e[maxn*2]; //边的链表
int head[maxn],dis[maxn],cnt;
bool vis[maxn];
int n,a,b;
inline void add_edge(int u,int v,int d){
cnt++;//把边加进去
e[cnt].dis=d;
e[cnt].to=v;
e[cnt].next=head[u];
head[u]=cnt;//存储上一条边
}
struct node{
int dis;//点的结构体,dis为A点到这个点的距离
int pos;
bool operator <(const node &x)const
{
return x.dis<dis;//重载运算符,要不然c++没法比
}
};
priority_queue<node> q;
inline void dij(){
dis[a]=0;
q.push((node){0,a});
while(!q.empty()){
node tmp=q.top();
q.pop();
int x=tmp.pos,d=tmp.dis;
if(vis[x]) continue;
vis[x]=1;
for(int i=head[x];i;i=e[i].next){
int y=e[i].to;
if(dis[y]>dis[x]+e[i].dis){
dis[y]=dis[x]+e[i].dis; //松弛
if(!vis[y]){
q.push((node){dis[y],y});//入队
}
}
}
}
}
我代码好丑



 浙公网安备 33010602011771号
浙公网安备 33010602011771号