CDQ分治笔记
CDQ分治(超级分治!)
这玩意是啥
一种分治思想,主要用于求偏序问题,前提是离线。OI wiki
大概思路
如图所示(网上找的,如有侵权请联系我我火速删除):
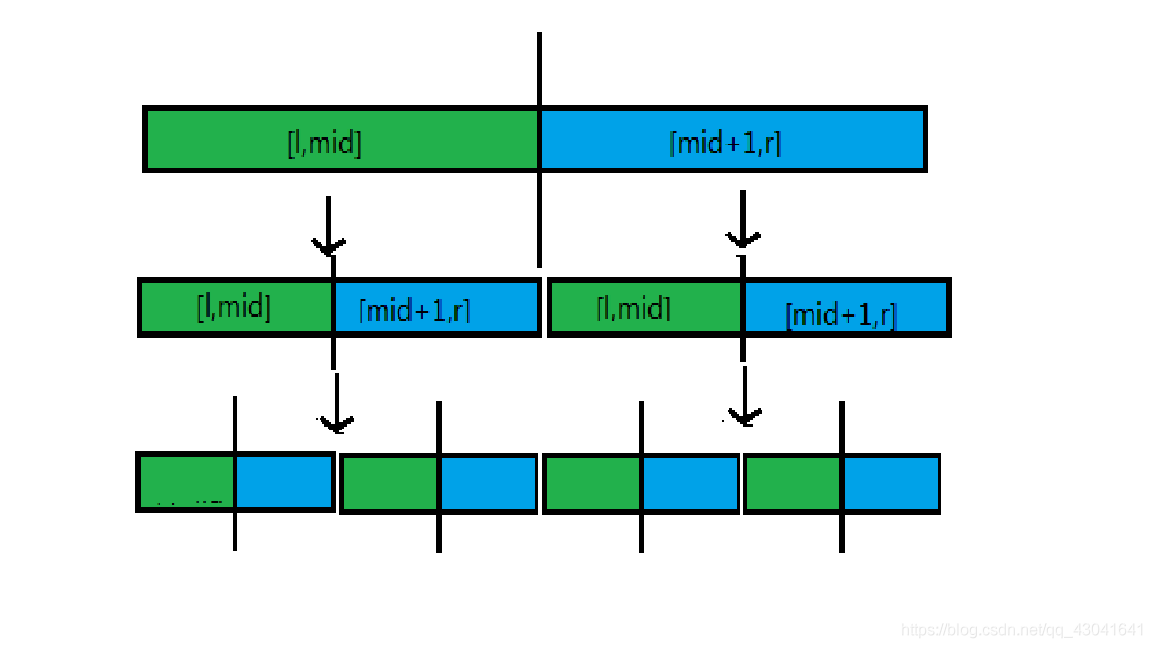
- 将一个区间 \(\left[l,r\right]\) 向下二分成两个区间 \(\left[l,mid\right]\) 和 \(\left[mid+1,r\right]\)
- 分到底之后返回,返回时分别处理分下去的这两个区间,以当前元素的值为下标,当前元素出现的个数为权值加入树状数组。
- 通过某种
骚气神奇的操作合并两个区间,这个操作待会会讲
其实这玩意看起来跟归并排序差不多,毕竟都是分下去合起来。
用树状数组是因为求前缀和灰常方便。
用一道例题来讲讲具体操作吧
例题
题意:
有 $ n $ 个元素,第 $ i $ 个元素有 $ a_i,b_i,c_i $ 三个属性,设 $ f(i) $ 表示满足 $ a_j \leq a_i $ 且 $ b_j \leq b_i $ 且 $ c_j \leq c_i $ 且 $ j \ne i $ 的 \(j\) 的数量。
对于 $ d \in [0, n) $,求 $ f(i) = d $ 的数量。
解法
对于每个元素我们用结构体记录它的 \(a,b,c,cnt,ans\) ,\(a,b,c\) 是题目中给出的,不解释;\(cnt\) 是跟这个元素相同元素的个数(包括它本身),\(ans\) 是这个元素目前找到的比它小的元素个数。
struct node{
int a,b,c,cnt,ans;
}s1[maxn],s2[maxn];
首先我们对第一维进行排序,使初始数组在第一维上变的有序,这样我们在之后的求解过程中就可以少考虑一个维度。
bool cmp1(node x,node y){
if(x.a!=y.a) return x.a<y.a;
if(x.b!=y.b) return x.b<y.b;
return x.c<y.c;
}
排序完毕后我们进行一个重的去,把相同的元素合并成一个并记录相同的个数,这样之后的分治中就很方便了
sort(s1+1,s1+1+n,cmp1);
for(int i=1;i<=n;++i){//去重
top++;//相同元素的个数
if(s1[i].a!=s1[i+1].a||s1[i].b!=s1[i+1].b||s1[i].c!=s1[i+1].c){
m++;
//s2是去重后的数组
s2[m].a=s1[i].a;
s2[m].b=s1[i].b;
s2[m].c=s1[i].c;
s2[m].cnt=top;
top=0;
}
}
然后我们就来到了重头戏——CDQ分治!
首先就跟普通的分治一样,先找出mid并向下二分小区间,然后合并的时候我们把小区间按照第二维排个序,因为之后要拿双指针遍历两个小区间,而双指针的前提是区间有序,所以这里我们要排一下序
bool cmp2(node x,node y){
if(x.b!=y.b) return x.b<y.b;
return x.c<y.c;
}
然后用双指针遍历两个小区间统计答案,\(i\) 遍历右边的从 \(mid+1\) 到 \(r\) 的区间,\(j\) 遍历左边的从 \(l\) 到 \(mid\) 的区间,因为前面第一、二维度都已经排好序了,所以我们可以直接判断第三维度。这里用树状数组维护答案,如果数对 \(\left(s2[i],s2[j]\right)\) 满足第二维度的条件,那就将 \(s2[j]\) 的值作为下标,\(s2[j]\) 的 \(cnt\) 作为权值加入到树状数组中,因为是前缀和,所以后面计算答案的时候只有当 \(s2[j]\) 的 \(c\) 小于 \(s2[i]\) 的 \(c\) 也就是满足第三维度的条件时才会计入答案。
int i,j=l;
for(i=mid+1;i<=r;++i){
while(s2[i].b>=s2[j].b&&j<=mid){
add(s2[j].c,s2[j].cnt);
++j;
}
s2[i].ans+=query(s2[i].c);
}//类似于归并的操作
最后别忘记清空树状数组多测不清空,爆零两行泪。
for(i=l;i<j;++i) add(s2[i].c,-s2[i].cnt);
应该也能用 \(memset\) 不过这俩时间复杂度都差不多。
最后计算 \(ans\) 这里有点复杂,题目中要求对于 $ d \in [0, n) \(,\) f(i) = d $ 的数量,所以我们就开一个 \(ans\) 数组(不会和结构体里的 \(ans\) 重名的ovo),对于下标 \(i\),\(ans[s2[i].ans+s2[i].cnt-1]+=s2[i].cnt\),为啥要这么做呢,这个 \(ans\) 数组的下标 \(i\) 代表 \(f(x) = i\) 的元素的个数,因为 \(s2[i].ans\) 表示比 \(s2[i]\) 小的元素个数,\(s2[i].cnt\) 表示和 \(s2[i]\) 相等的元素个数,\(-1\) 是因为要减去它本身。
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#ifdef ONLINE_JUDGE
#define debug(x)
#else
#define debug(x) cout<<' '<<#x<<'='<<x<<endl;
#endif
using namespace std;
inline int read(){
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9'){
x=(x<<3)+(x<<1)+(c^48);
c=getchar();
}
return x*f;
}
inline void write(int x){
if(x<0){x=-x;putchar('-');}
if(x>9) write(x/10);
putchar(x%10+'0');
}
const int maxn=200005;
struct node{
int a,b,c,cnt,ans;
}s1[maxn],s2[maxn];
int n,m,k,mx,top,ans[maxn];
int c[maxn];
//第一维排序
bool cmp1(node x,node y){
if(x.a!=y.a) return x.a<y.a;
if(x.b!=y.b) return x.b<y.b;
return x.c<y.c;
}
//第二维排序,给双指针做前提
bool cmp2(node x,node y){
if(x.b!=y.b) return x.b<y.b;
return x.c<y.c;
}
//------树状数组------
inline int lowbit(int x){
return x&(-x);
}
void add(int x,int y){
while(x<=mx){
c[x]+=y;
x+=lowbit(x);
}
}
inline int query(int x){
int sum=0;
while(x){
sum+=c[x];
x-=lowbit(x);
}
return sum;
}
//最重要的cdq
void cdq(int l,int r){
//如果分到最小那就return
if(l==r) return;
int mid=(l+r)>>1;
//向下二分
cdq(l,mid);
cdq(mid+1,r);
//合并回来排序
sort(s2+l,s2+mid+1,cmp2);
sort(s2+mid+1,s2+r+1,cmp2);
int i,j=l;
//双指针遍历两个区间
for(i=mid+1;i<=r;++i){
while(s2[i].b>=s2[j].b&&j<=mid){
add(s2[j].c,s2[j].cnt);
++j;
}
//前缀和只计算比s2[i].c小的
s2[i].ans+=query(s2[i].c);
}//类似于归并的操作
//清空树状数组
for(i=l;i<j;++i) add(s2[i].c,-s2[i].cnt);
}
int main()
{
n=read();
k=read();
mx=k;//树状数组的区间
for(int i=1;i<=n;++i){
s1[i].a=read();
s1[i].b=read();
s1[i].c=read();
}
sort(s1+1,s1+1+n,cmp1);
for(int i=1;i<=n;++i){//去重
top++;
if(s1[i].a!=s1[i+1].a||s1[i].b!=s1[i+1].b||s1[i].c!=s1[i+1].c){
m++;
s2[m].a=s1[i].a;
s2[m].b=s1[i].b;
s2[m].c=s1[i].c;
s2[m].cnt=top;
top=0;
}
}
cdq(1,m);
for(int i=1;i<=m;++i)
ans[s2[i].ans+s2[i].cnt-1]+=s2[i].cnt;
for(int i=0;i<n;++i) write(ans[i]),putchar('\n');
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号