【工程实践】go语言实现MerkleTree
简介
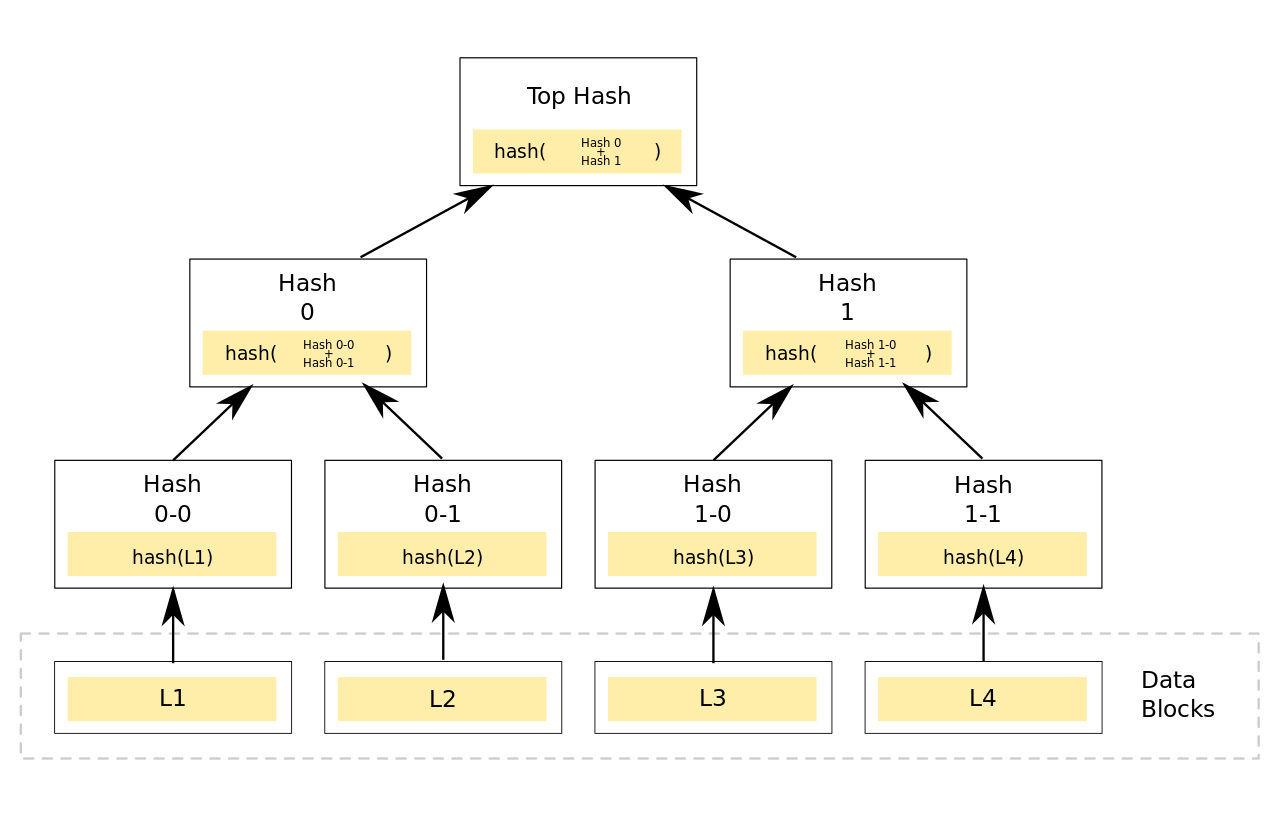
默克尔树(MerkleTree)是一种典型的二叉树结构,其主要特点为:
- 最下面的叶节点包含存储数据或其哈希值;
- 非叶子节点(包括中间节点和根节点)的内容为它的两个孩子节点内容的哈希值。
所以底层数据的任何变动,都会传递到其父节点,一层层沿着路径一直到树根。这意味树根的值实际上代表了对底层所有数据的“数字摘要”。
代码实现
package main
import (
"bytes"
"crypto/sha256"
"encoding/hex"
"fmt"
)
// MerkleTree 节点
type MerkleNode struct {
Left *MerkleNode
Right *MerkleNode
Data []byte
}
// MerkleTree 根
type MerkleTree struct {
RootNode *MerkleNode
}
// 创建Merkle节点
func NewMerkleNode(left, right *MerkleNode, data []byte) *MerkleNode {
node := MerkleNode{}
// 创建存储明文信息的叶子节点
if left == nil && right == nil {
node.Data = data
// 创建只有一个分支的MerkleNode
} else if left != nil && right == nil {
hash := sha256.Sum256(left.Data)
node.Data = hash[:]
// 创建有两个分支的MerkleNode
} else {
// slice = append(slice, anotherSlice...) 两个slice拼接在一起时要加...
hash := sha256.Sum256(append(left.Data, right.Data...))
node.Data = hash[:]
}
node.Left = left
node.Right = right
return &node
}
func NewMerkleTree(data [][]byte) *MerkleTree {
var nodes []MerkleNode
// 将所有数据构建为dataNode节点,接入node节点的左分支,并将node节存到nodes数组中
for _, datum := range data {
dataNode := NewMerkleNode(nil, nil, datum)
node := NewMerkleNode(dataNode, nil, nil)
nodes = append(nodes, *node)
}
for {
var newLevel []MerkleNode
// 根据当前层的节点,构造上一层
// 当前层节点为奇数时
if len(nodes)%2 == 1 {
for j := 0; j < len(nodes)-1; j += 2 {
node := NewMerkleNode(&nodes[j], &nodes[j+1], nil)
newLevel = append(newLevel, *node)
}
node := NewMerkleNode(&nodes[len(nodes)-1], nil, nil)
newLevel = append(newLevel, *node)
// 当前层节点为偶数时
} else {
for j := 0; j < len(nodes); j += 2 {
node := NewMerkleNode(&nodes[j], &nodes[j+1], nil)
newLevel = append(newLevel, *node)
}
}
// 更新层节点
nodes = newLevel
if len(nodes) == 1 {
break
}
}
mTree := MerkleTree{&nodes[0]}
return &mTree
}
// 先序遍历输出所有节点
func showMeerkleTree(root *MerkleNode) {
if root == nil {
return
} else {
PrintNode(root)
}
showMeerkleTree(root.Left)
showMeerkleTree(root.Right)
}
func PrintNode(node *MerkleNode) {
fmt.Printf("%p\n", node)
// 输出存储信息明文节点
if node.Left != nil || node.Right != nil {
fmt.Printf("left[%p], right[%p], data(%v)\n", node.Left, node.Right, hex.EncodeToString(node.Data))
// 输出存储哈希值的节点
} else if node.Left == nil || node.Right == nil {
fmt.Printf("left[%p], right[%p], data(%v)\n", node.Left, node.Right, string(node.Data))
}
}
// 检查是否满足MerkleTree的条件
func check(node *MerkleNode) bool {
var hashByte32 [32]byte
if node.Left == nil && node.Right == nil {
return true
} else if node.Left != nil && node.Right == nil {
hashByte32 = sha256.Sum256(node.Left.Data)
} else {
hashByte32 = sha256.Sum256(append(node.Left.Data, node.Right.Data...))
}
hash := hashByte32[:]
result := bytes.Equal(hash, node.Data)
fmt.Printf("Is this a MerkleTree? : %v", result)
return result
}
func main() {
data := [][]byte{[]byte("node1"), []byte("node2"), []byte("node3"), []byte("node4"),
[]byte("node5")}
tree := NewMerkleTree(data)
showMeerkleTree(tree.RootNode)
check(tree.RootNode)
}
输出内容为
0xc0001077a0
left[0xc0001360a0], right[0xc0001360c8], data(e84479b93fed1c8d912b865a7508f42e1e3dc777649cc80ccf59733f1982f40d)
0xc0001360a0
left[0xc0001380a0], right[0xc0001380c8], data(b698d822f9dbf3099c0aa30ba8120f48f3c92753be4eedb3f8cc99eb934cc3fb)
0xc0001380a0
left[0xc00013a000], right[0xc00013a028], data(64b04b718d8b7c5b6fd17f7ec221945c034cfce3be4118da33244966150c4bd4)
0xc00013a000
left[0xc000107410], right[0x0], data(ca12f31b8cbf5f29e268ea64c20a37f3d50b539d891db0c3ebc7c0f66b1fb98a)
0xc000107410
left[0x0], right[0x0], data(node1)
0xc00013a028
left[0xc0001074a0], right[0x0], data(15b18a7243257695704f66a3b1ddc9311194fc7d2e1896f440cc517c777ab7ec)
0xc0001074a0
left[0x0], right[0x0], data(node2)
0xc0001380c8
left[0xc00013a050], right[0xc00013a078], data(30304ac1e6721c1f197ff47b1682794872701e823bc962b79682ce66d3283783)
0xc00013a050
left[0xc000107500], right[0x0], data(3b5bb1c6e7b76daba8afd89516e24140a67fc6be2ba071cc3b97d1b2e08c238d)
0xc000107500
left[0x0], right[0x0], data(node3)
0xc00013a078
left[0xc000107560], right[0x0], data(d2b8f62a7e335bbd5576c8422844760f22ec378009eeea790c41e4dc45f23c33)
0xc000107560
left[0x0], right[0x0], data(node4)
0xc0001360c8
left[0xc0001380f0], right[0x0], data(2a6e2bd6658e6ce0f9f0abb6bc668a997c14e8f5465fcd4cd19678ae0e4dd087)
0xc0001380f0
left[0xc00013a0a0], right[0x0], data(31e81bb6828abbf114edb182849cc89deac585d320f5a1a33d054ca047616a5c)
0xc00013a0a0
left[0xc0001075c0], right[0x0], data(23af406016994347aaa3e894e9a820049ace3656406fb06e7636b692db56026f)
0xc0001075c0
left[0x0], right[0x0], data(node5)
Is this a MerkleTree? : true

