hdu1056
果然是数学题，感觉就是阅读题，加上小小的思维
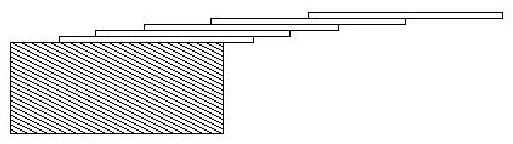
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.
The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.
For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.
The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.
For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.
Sample Input
1.00 3.71 0.04 5.19 0.00
Sample Output
3 card(s) 61 card(s) 1 card(s) 273 card(s)
是一道水题：
代码：
#include<iostream>
using namespace std;
int main()
{
double sum,sum1;
int k;
while(cin>>sum){
if(sum==0.00)
break;
sum1=0;
k=0;
while(sum>sum1){
sum1+=(1.0/(k+2));
k++;
// cout<<k<<' ';
}
cout<<k<<' '<<"card(s)"<<endl;
}
return 0;
}
using namespace std;
int main()
{
double sum,sum1;
int k;
while(cin>>sum){
if(sum==0.00)
break;
sum1=0;
k=0;
while(sum>sum1){
sum1+=(1.0/(k+2));
k++;
// cout<<k<<' ';
}
cout<<k<<' '<<"card(s)"<<endl;
}
return 0;
}
但是你们知道吗
#include<iostream>
using namespace std;
int main()
{
double sum,sum1;
double k;
while(cin>>sum){
if(sum==0.00)
break;
sum1=0;
k=0;
while(sum>sum1){
sum1+=(1/(k+2));
k++;
// cout<<k<<' ';
}
cout<<k<<' '<<"card(s)"<<endl;
}
return 0;
}这样却t了
using namespace std;
int main()
{
double sum,sum1;
double k;
while(cin>>sum){
if(sum==0.00)
break;
sum1=0;
k=0;
while(sum>sum1){
sum1+=(1/(k+2));
k++;
// cout<<k<<' ';
}
cout<<k<<' '<<"card(s)"<<endl;
}
return 0;
}这样却t了
也就是说int k
1.0/(k+1)
比
double k
1/（k+1）
省很多的时间
一个440ms
一个t了
