Kefa and Company

Kefa and Company

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Kefa wants to celebrate his first big salary by going to restaurant. However, he needs company.

Kefa has n friends, each friend will agree to go to the restaurant if Kefa asks. Each friend is characterized by the amount of money he has and the friendship factor in respect to Kefa. The parrot doesn't want any friend to feel poor compared to somebody else in the company (Kefa doesn't count). A friend feels poor if in the company there is someone who has at least d units of money more than he does. Also, Kefa wants the total friendship factor of the members of the company to be maximum. Help him invite an optimal company!

Input

The first line of the input contains two space-separated integers, n and d (1 ≤ n ≤ 105, 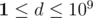) — the number of Kefa's friends and the minimum difference between the amount of money in order to feel poor, respectively.

Next n lines contain the descriptions of Kefa's friends, the (i + 1)-th line contains the description of the i-th friend of type mi, si(0 ≤ mi, si ≤ 109) — the amount of money and the friendship factor, respectively.

Output

Print the maximum total friendship factir that can be reached.

Sample test(s)

input

4 5
75 5
0 100
150 20
75 1

output

100

input

5 100
0 7
11 32
99 10
46 8
87 54

output

111

Note

In the first sample test the most profitable strategy is to form a company from only the second friend. At all other variants the total degree of friendship will be worse.

In the second sample test we can take all the friends.

 

#include<cstdio>
#include<algorithm>
#define ll __int64
using namespace std;
struct node{
    ll m,s;
    bool operator< (const node &x) const{
        return m < x.m;
    }
}a[100005];
ll b[100005];
ll sum[100005];
int main(){
    int n;
    ll d;
    scanf("%d%I64d",&n,&d);
    for(int i = 0; i < n; i++){
        scanf("%I64d%I64d",&a[i].m,&a[i].s);
    }
    sort(a,a+n);
    ll ans = 0;
    for(int i = 1; i <= n; i++){
        b[i-1] = a[i-1].m;
        sum[i] = sum[i-1] + a[i-1].s;
    }
    for(int i = 0; i < n; i++){
        int it = upper_bound(b,b+n,a[i].m + d - 1) - b;
        ll num = sum[it] - sum[i];
        ans = max(ans,num);
    }
    printf("%I64d\n",ans);
    return 0;
}