"Or" Game

"Or" Game

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given n numbers a1, a2, ..., an. You can perform at most k operations. For each operation you can multiply one of the numbers by x. We want to make 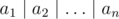 as large as possible, where  denotes the bitwise OR.

Find the maximum possible value of 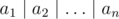 after performing at most k operations optimally.

Input

The first line contains three integers n, k and x (1 ≤ n ≤ 200 000, 1 ≤ k ≤ 10, 2 ≤ x ≤ 8).

The second line contains n integers a1, a2, ..., an (0 ≤ ai ≤ 109).

Output

Output the maximum value of a bitwise OR of sequence elements after performing operations.

Sample test(s)

input

3 1 2
1 1 1

output

3

input

4 2 3
1 2 4 8

output

79

Note

For the first sample, any possible choice of doing one operation will result the same three numbers 1, 1, 2 so the result is .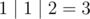

For the second sample if we multiply 8 by 3 two times we'll get 72. In this case the numbers will become 1, 2, 4, 72 so the OR value will be 79 and is the largest possible result.

 首先，这是一道贪心题;了解为什么贪心：

　　　　二进制位数越多，数字自然越大，x最小为2，每乘一次x，2进制位数至少加1;所以自然要将指定的一个数乘以(x^k)为最优;

其次，为什么不是直接最大值乘以(x^k):

　　　　这是或运算特性，渣渣说不上来 = =！举例 反证 ：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　2 1 2
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12 9
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　24|9 = 25; 12|18 = 30;

 

然后，学会预处理，可以减少很大的复杂度：

　　　　正着累加一边pre[i] = pre[i-1] | a[i];

　　　　倒着累加一边pre2[i] = pre[i+1] | a[i];

最后，依次比较pre[i-1]|(a[i]*x^k)|pre2[i+1],暴力即可。

复杂度为O(3n);

#include<cstdio>
#include<algorithm>
#define ll __int64
using namespace std;
ll a[200005];
ll pre[200005];
ll pre2[200005];
int main(){
    int n,k,x;
    scanf("%d%d%d",&n,&k,&x);
    int maxn = 0;
    int j = 0;
    for(int i = 1; i <= n; i++){
        scanf("%I64d",&a[i]);

    }
    int op = 1;
    while(k--)
        op *= x;
    ll ans = 0;
    for(int i = 1;i <= n; i++){
        pre[i] = pre[i-1]|a[i];
    }
    for(int i = n; i >= 1; i--){
        pre2[i] = pre2[i+1]|a[i];
    }
    for(int i = 1; i <= n; i++)
        ans = max(ans,pre[i-1]|(a[i]*op)|pre2[i+1]);
    printf("%I64d\n",ans);
    return 0;
}