POJ1703-Find them, Catch them
题目链接:点击打开链接
Find them, Catch them
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 51710 | Accepted: 15831 |
Description
The police office in Tadu City decides to say ends to the chaos, as launch actions to root up the TWO gangs in the city, Gang Dragon and Gang Snake. However, the police first needs to identify which gang a criminal belongs to. The present question is, given two criminals; do they belong to a same clan? You must give your judgment based on incomplete information. (Since the gangsters are always acting secretly.)
Assume N (N <= 10^5) criminals are currently in Tadu City, numbered from 1 to N. And of course, at least one of them belongs to Gang Dragon, and the same for Gang Snake. You will be given M (M <= 10^5) messages in sequence, which are in the following two kinds:
1. D [a] [b]
where [a] and [b] are the numbers of two criminals, and they belong to different gangs.
2. A [a] [b]
where [a] and [b] are the numbers of two criminals. This requires you to decide whether a and b belong to a same gang.
Input
The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case begins with a line with two integers N and M, followed by M lines each containing one message as described above.
Output
For each message "A [a] [b]" in each case, your program should give the judgment based on the information got before. The answers might be one of "In the same gang.", "In different gangs." and "Not sure yet."
Sample Input
1
5 5
A 1 2
D 1 2
A 1 2
D 2 4
A 1 4
Sample Output
Not sure yet.
In different gangs.
In the same gang.
题目大意:A操作是询问x和y的关系(3种之一),D操作说明x和y不在一个帮
思路:并查集,但是和普通并查集不一样。两种方法:①开两倍的空间,两个并查集。②用向量偏移写。
方法①:father[2*N], 1~N是龙帮,N+1~2N是蛇帮
AC代码:
#include<iostream>
#include<cstdio>
char s[2];
int T, n, m, u, v;
const int N = 100010;
int father[2*N];//两种关系
int rank[2*N];//树高(优化)
void init(int n) {
for(int i = 0; i <= n+1; i++) {
father[i] = i;
rank[i] = 0;
}
}
int find(int x) {//递归形式的路径压缩
if(father[x] == x) {
return x;
} else {
return father[x] = find(father[x]);
}
}
void Union(int x, int y) {//按秩合并
x = find(x);
y = find(y);
if(x == y)
return;
if(rank[x] < rank[y]) {//树高的为祖先
father[x] = y;
} else {
father[y] = x;
if(rank[x] == rank[y])//一样高 rank++
rank[x]++;
}
}
int main() {
scanf("%d", &T);
while(T--) {
scanf("%d%d", &n, &m);
init(2*n);
for(int i = 0; i < m; i++) {
scanf("%s%d%d", s, &u, &v);
if(s[0] == 'D') {//不在一个集合 把两种情况都合并了
Union(u+n, v); //u在蛇,v在龙
Union(u, v+n);//u在龙,v在蛇
} else {
if(find(u) == find(v) || find(u+n) == find(v+n))//把集合扩大,分为两部分,然后查询。 //在同一个帮派
printf("In the same gang.\n");
else if(find(u) == find(v+n) || find(u+n) == find(v))//不在一个帮派
printf("In different gangs.\n");
else
printf("Not sure yet.\n");
}
}
}
}
方法②:向量偏移方法,该方法不是太熟悉,只是自己梳理一下。
参考博客:https://blog.csdn.net/freezhanacmore/article/details/8774033
之所以叫向量偏移,肯定是和向量有关系。
先从find函数说起,find函数在找父亲节点的同时,更新了整体的关系。这个公式是可以由假设关系推出来的。
设a与b的关系为r1,b与c的关系是r2,那么a与c的关系就是(r1+r2)%2;
列表,枚举所有关系,可以看出来这个规律。(具体参考上面博客)
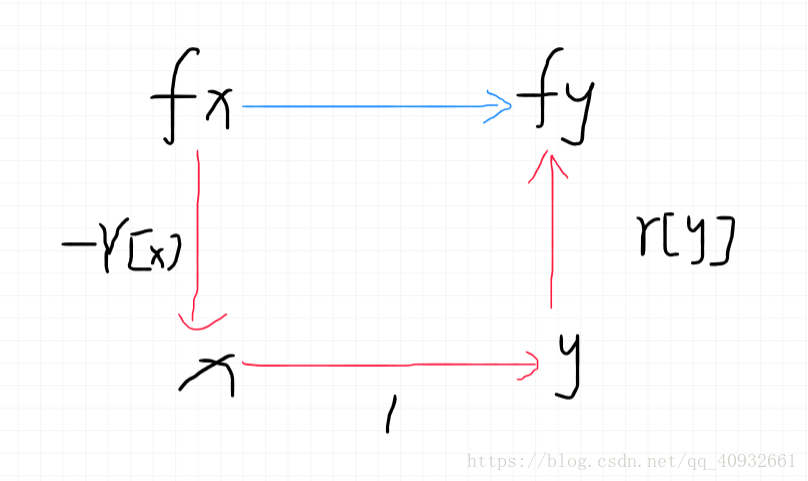
再说Union函数 ,把fx合并到fy,那么fx 对 fy的关系 见下图
x对y的关系为1,(同类为0),不同类才合并
#include<iostream>
#include<cstdio>
using namespace std;
const int MAX = 100010;
int flag[MAX];
int father[MAX];//存该点的根节点
int rank[MAX];
//不知道和食物链的有什么区别,这里可以用rank数组
void init(int n) {
for(int i = 0; i <= n + 1; i++) {
father[i] = i;
flag[i] = 0;
rank[i] = 0;
}
}
int find(int x) {
if(father[x] == x)
return x;
int xx = father[x];
father[x] = find(father[x]);
flag[x] = (flag[x] + flag[xx]) % 2;// 自己与爷爷 =(自己与父亲 + 父亲与爷爷)%2
return father[x];
}
void Union(int x, int y) {
int fx = find(x);
int fy = find(y);
if(fx == fy){
return;
}
if(rank[fx] < rank[fy]) {//注意这里的x和fx 容易写错
father[fx] = fy;
flag[fx] = (flag[y] - flag[x] + 1) % 2;
} else {
father[fy] = fx;
flag[fy] = (flag[x] - flag[y] + 1) % 2;
if(rank[fx] == rank[fy])
rank[fx]++;
}
}
int T, u, v, n, m;
int main() {
scanf("%d", &T);
while(T--) {
scanf("%d%d", &n, &m);
init(n);
while(m--) {//合并
char ch[2];
scanf("%s%d%d", ch, &u, &v);//巨坑!!!cin超时
if(ch[0] == 'A') {
if(find(u) != find(v))
printf("Not sure yet.\n");
else {
if(flag[u] != flag[v])
printf("In different gangs.\n");
else
printf("In the same gang.\n");
}
} else {
Union(u, v);
}
}
}
return 0;
}




