2019牛客暑期多校训练营（第二场）

Solutions

---

A：Eddy Walker

题意：

给出$n$个点，编号为$0\sim n-1$，问走完所有点恰巧到达$m$点的概率。

思路：

如果，只要$m$不为$0$，到其他点概率都是一样的，为$\frac1{n-1}$，然后判$m=0$的情况。

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;

ll q_pow(ll a,ll b) {
    ll ans=1;
    ll tmp=a%mod;
    while(b) {
        if(b&1) ans=ans*tmp%mod;
        tmp=tmp*tmp%mod;
        b=b>>1;
    }
    return ans;
}

int main() {
    #ifdef DEBUG
    freopen("in.txt","r",stdin);
    #endif
    int _;
    ll ans=1;
    for(scanf("%d",&_);_;_--) {
        ll n,m;
        scanf("%lld%lld",&n,&m);
        if(n==1&&m==0) ans*=1;
        else if(m==0&&n>1) ans=0;
        else ans=ans*q_pow(n-1,mod-2)%mod;
        printf("%lld\n",ans);
    }
}

B：Eddy Walker 2

题意：

某人开始在$0$点，给出目标点$k$，和每步能走的最大距离$k$，且走距离$1\sim k$概率都为$\frac1k$，求最后到达$n$点的概率，$n=-1$表示无穷远。

思路：

$dp[i]$表示到达$i$点的概率，那么

$dp[i]=\frac1k\sum_{j=i-k}^{i-1}dp[j]$，线性递推式，丢进BM里搞一搞

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <cassert>
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
typedef vector<int> VI;
typedef long long ll;
typedef pair<int,int> PII;
const ll mod=1000000007;
ll powmod(ll a,ll b) {ll res=1;a%=mod; assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
// head

namespace linear_seq {
    const int N=10010;
    ll res[N],base[N],_c[N],_md[N];

    vector<int> Md;
    void mul(ll *a,ll *b,int k) {
        rep(i,0,k+k) _c[i]=0;
        rep(i,0,k) if (a[i]) rep(j,0,k) _c[i+j]=(_c[i+j]+a[i]*b[j])%mod;
        for (int i=k+k-1;i>=k;i--) if (_c[i])
            rep(j,0,SZ(Md)) _c[i-k+Md[j]]=(_c[i-k+Md[j]]-_c[i]*_md[Md[j]])%mod;
        rep(i,0,k) a[i]=_c[i];
    }
    int solve(ll n,VI a,VI b) { // a 系数 b 初值 b[n+1]=a[0]*b[n]+...
        ll ans=0,pnt=0;
        int k=SZ(a);
        assert(SZ(a)==SZ(b));
        rep(i,0,k) _md[k-1-i]=-a[i];_md[k]=1;
        Md.clear();
        rep(i,0,k) if (_md[i]!=0) Md.push_back(i);
        rep(i,0,k) res[i]=base[i]=0;
        res[0]=1;
        while ((1ll<<pnt)<=n) pnt++;
        for (int p=pnt;p>=0;p--) {
            mul(res,res,k);
            if ((n>>p)&1) {
                for (int i=k-1;i>=0;i--) res[i+1]=res[i];res[0]=0;
                rep(j,0,SZ(Md)) res[Md[j]]=(res[Md[j]]-res[k]*_md[Md[j]])%mod;
            }
        }
        rep(i,0,k) ans=(ans+res[i]*b[i])%mod;
        if (ans<0) ans+=mod;
        return ans;
    }
    VI BM(VI s) {
        VI C(1,1),B(1,1);
        int L=0,m=1,b=1;
        rep(n,0,SZ(s)) {
            ll d=0;
            rep(i,0,L+1) d=(d+(ll)C[i]*s[n-i])%mod;
            if (d==0) ++m;
            else if (2*L<=n) {
                VI T=C;
                ll c=mod-d*powmod(b,mod-2)%mod;
                while (SZ(C)<SZ(B)+m) C.pb(0);
                rep(i,0,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
                L=n+1-L; B=T; b=d; m=1;
            } else {
                ll c=mod-d*powmod(b,mod-2)%mod;
                while (SZ(C)<SZ(B)+m) C.pb(0);
                rep(i,0,SZ(B)) C[i+m]=(C[i+m]+c*B[i])%mod;
                ++m;
            }
        }
        return C;
    }
    int gao(VI a,ll n) {
        VI c=BM(a);
        c.erase(c.begin());
        rep(i,0,SZ(c)) c[i]=(mod-c[i])%mod;
        return solve(n,c,VI(a.begin(),a.begin()+SZ(c)));
    }
};

ll dp[3000];
int main() {
    int _;
    for(scanf("%d",&_);_;_--) {
        int k;
        ll n;
        scanf("%d%lld",&k,&n);
        if(n==-1) {
            printf("%lld\n",2*powmod(k+1,mod-2)%mod);
        } else {
            VI t;
            dp[0]=1;
            t.push_back(dp[0]);
            for(int i=1;i<=2*k;i++) {
                dp[i]=0;
                for(int j=max(0,i-k);j<i;j++) {
                    dp[i]=(dp[i]+dp[j])%mod;
                }
                dp[i]=dp[i]*powmod(k,mod-2)%mod;
                t.push_back(dp[i]);
            }
            printf("%lld\n",linear_seq::gao(t,n));
        }
    }
}

D：Kth Minimum Clique

题意：

给出$n$个点以及点权，求第$k$小团。空团是第一小。

思路：

可以拿着空的，往里面放。每次取出最小的，往里放点，放的时候判断一下是否和团里面的都有边，判断可以用$bitset$优化

放的时候，编号递增的放，防止放入重复点。

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;

struct Node{
    ll w;
    bitset<110> S;
    bool operator < (const Node& b) const {
        return w>b.w;
    }
};

char buf[110];
bitset<110> bs[110];
ll a[110];

int main() {
    #ifdef DEBUG
    freopen("in.txt","r",stdin);
    #endif
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++) scanf("%lld",&a[i]);
    for(int i=0;i<n;i++) {
        scanf("%s",buf);
        for(int j=0;buf[j];j++) {
            if(buf[j]=='1') bs[i][j]=1;
        }
    }
    priority_queue<Node> pq;
    bitset<110> t;
    pq.push((Node){0,t});
    while(!pq.empty()) {
        Node f=pq.top();pq.pop();
        bitset<110> r=f.S;
        k--;
        if(k==0) {
            printf("%lld\n",f.w);
            return 0;
        }
        int pos=0;
        for(int i=0;i<n;i++) {
            if(r[i]) {
                pos=i+1;
            }
        }
        for(int i=pos;i<n;i++) {
            if(!r[i]&&(bs[i]&r)==r) {
                r[i]=1;
                pq.push((Node){f.w+a[i],r});
                r[i]=0;
            }
        }
    }
    puts("-1");
}

E：MAZE

题意：

有一个$n\times\ m$的$01$矩阵，$1$表示不可行，$0$表示可行

每次可以从$\left(i,j\right)$走到$\left(i,j-1\right),\left(i,j+1\right),\left(i+1,j\right)$，且不能回到走过的格子

有$q$个以下两种欧冠操作：

1. 将某个格子的状态反转
2. 询问从$\left(1,x\right)走到\left(n,y\right)$的方案数

• $1\leq\ n$，$q\leq\ 5e4$，$1\leq\ m\leq10$

思路：

参考1、2、3Bolgs

先不考虑修改，设$a[i][j]$表示第$i$行第$j$个元素

$dp[i][j]$表示能从第$i-1$行经过$\left(i-1,j\right)$走到$\left(i,j\right)$的方案数，状态转移方程如下：

$dp[i][j]=\sum_{k=1}^{j-1}{dp[i-1][k]}_{for\ a[i-1][k]=0} +\sum_{k=j}^m\ {dp[i-1][k]}_{for\ a[i-1][k]=0}$

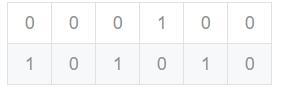
比如，$n=2,m=6$时，

$dp[2][2]=dp[1][1]+dp[1][2]+dp[1][3]$

$dp[2][6]=dp[1][5]+dp[1][6]$

我们可以用“列可达”矩阵表示转移关系，然后乘起来就是最后的结果。

“列可达”比如第一行的列可达，第一列为$0$，所以$\left(0,0\right)$位置为$1$，它能到达$2,3$列所以$\left(2,1\right),\left(3,1\right)$为$1$，遇到$1$结束。（见下图）

依次类推。

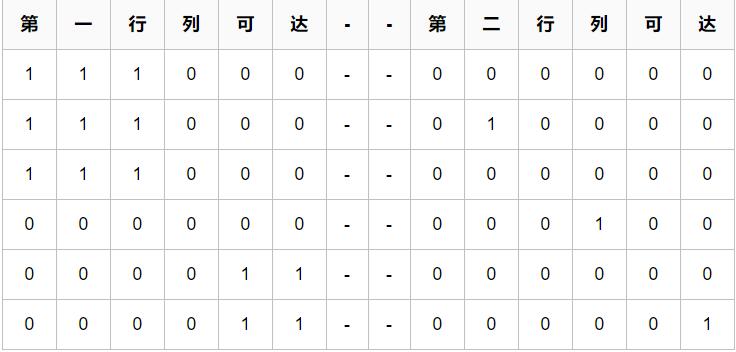
也就是这样：

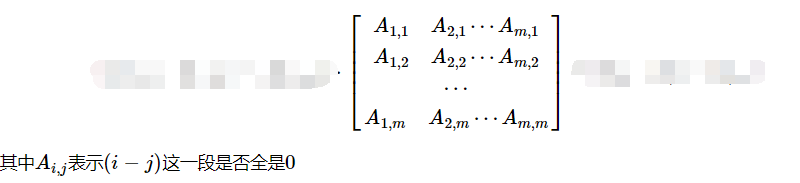
发现两个矩阵相乘就可以查询答案了。可以用线段树维护矩阵相乘，每个节点维护一个矩阵（一行）。

修改的话，就修改维护那一行的节点。

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
const int N=50010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;

int n,m,a[N][15];

struct Mat{
    ll a[15][15];
    void init() {memset(a,0,sizeof(a));}
    Mat operator * (const Mat &b)const {
        Mat ans;
        ans.init();
        for(int i=1;i<=m;i++) {
            for(int j=1;j<=m;j++) {
                for(int k=1;k<=m;k++) {
                    ans.a[i][j]=(ans.a[i][j]+a[i][k]*b.a[k][j]%mod)%mod;
                }
            }
        }
        return ans;
    }
}mat[N<<2];

void mul(int rt,int x) {
    mat[rt].init();
    for(int i=1;i<=m;i++) {
        if(a[x][i]) continue;
        mat[rt].a[i][i]=1;
        for(int k=i+1;k<=m&&(!a[x][k]);k++)
            mat[rt].a[k][i]=1;
        for(int k=i-1;k>=1&&(!a[x][k]);k--)
            mat[rt].a[k][i]=1;
    }
}

void build(int l,int r,int rt) {
    if(l==r) {
        mul(rt,l);
        return ;
    }
    int mid=(l+r)>>1;
    build(l,mid,rt<<1);
    build(mid+1,r,rt<<1|1);
    mat[rt]=mat[rt<<1]*mat[rt<<1|1];
}

void updata(int v,int l,int r,int rt) {
    if(l==r) {
        mul(rt,l);
        return ;
    }
    int mid=(l+r)>>1;
    if(v<=mid) updata(v,l,mid,rt<<1);
    else updata(v,mid+1,r,rt<<1|1);
    mat[rt]=mat[rt<<1]*mat[rt<<1|1];
}

int main() {
    #ifdef DEBUG
    freopen("in.txt","r",stdin);
    #endif
    int q;
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++) {
        for(int j=1;j<=m;j++)
            scanf("%1d",&a[i][j]);
    }
    build(1,n,1);
    while(q--) {
        int op,x,y;
        scanf("%d%d%d",&op,&x,&y);
        if(op==1) {
            a[x][y]^=1;
            updata(x,1,n,1);
        } else printf("%lld\n",mat[1].a[x][y]);
    }
    return 0;
}

F：Partition problem

题意：

$2n$个人，每个人都与其他人有对抗值，分成两个集合且集合大小相等，求分配后的最大对抗值

思路：

啥都不说，就是不会$DFS$，感觉还做过。给出链接

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;

ll a[30][30],ans;
int sa[30],sb[30];
int n;

void dfs(int id,int num1,int num2,ll sum) {
    if(num1==n&&num2==n) {
        for(int i=0;i<num1;i++) printf("%d ",sa[num1]);
        puts("");
        for(int i=0;i<num2;i++) printf("%d ",sb[num2]);
        puts("");
        ans=max(ans,sum);
        return;
    }
    if(num1<n) {
        ll tmp=0;
        for(int i=0;i<num2;i++) tmp+=a[id][sb[i]];
        sa[num1]=id;
        dfs(id+1,num1+1,num2,sum+tmp);
    }
    if(num2<n) {
        ll tmp=0;
        for(int i=0;i<num1;i++) tmp+=a[id][sa[i]];
        sb[num2]=id;
        dfs(id+1,num1,num2+1,sum+tmp);
    }
}
int main() {
    #ifdef DEBUG
    freopen("in.txt","r",stdin);
    #endif
    scanf("%d",&n);
    for(int i=1;i<=2*n;i++) {
        for(int j=1;j<=2*n;j++)
            scanf("%lld",&a[i][j]);
    }
    dfs(1,0,0,0);
    printf("%lld\n",ans);
}

 

H：Second Large Rectangle

题意：

求次大全$1$矩阵的面积。

思路：

首先最大全$1$矩阵可以通过单调栈求出，用同样的方法，把二维的压下来，每一行存当前高度，然后每一行都用单调栈维护，求得的矩阵去更新答案，注意！！！$x\ast(y-1),y\ast(x-1)$也要更新答案。。。当时没理解，加入就AC了。。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=100010;
const int inf=0x3f3f3f3f;

int a[1010][1010];
int n,m;
stack<pair<int,int> > s;
vector<int> ansans;
int main() {
    while(~scanf("%d%d",&n,&m)) {
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=m;j++) {
                scanf("%1d",&a[i][j]);
                if(a[i][j]) a[i][j]+=a[i-1][j];
            }
            a[i][m+1]=0;
        }
        pair<int,int> v;
        for(int i=1;i<=n;i++) {
            for(int j=1;j<=m+1;j++) {
                if(s.empty()||s.top().second<=a[i][j]) {
                    s.push({1,a[i][j]});
                }
                else {
                    int sum=0;
                    while(!s.empty()&&s.top().second>a[i][j]) {
                        v=s.top();
                        sum+=v.first;
                        int area1=sum*v.second;
                        int area2=(sum-1)*v.second;
                        int area3=sum*(v.second-1);
                        ansans.push_back(area1);
                        ansans.push_back(area2);
                        ansans.push_back(area3);
                        s.pop();
                    }
                    s.push({sum+1,a[i][j]});
                }
            }
            while(!s.empty()) s.pop();
        }
        sort(ansans.begin(),ansans.end());
        int len=ansans.size();
        if(len<2) printf("0\n");
        else {
            printf("%d\n",ansans[len-2]);
        }
        while(!s.empty()) s.pop();
        ansans.clear();
    }
}