BZOJ1497 最大获利
Description
新的技术正冲击着手机通讯市场,对于各大运营商来说,这既是机遇,更是挑战。THU集团旗下的CS&T通讯公司在新一代通讯技术血战的前夜,需要做太多的准备工作,仅就站址选择一项,就需要完成前期市场研究、站址勘测、最优化等项目。在前期市场调查和站址勘测之后,公司得到了一共N个可以作为通讯信号中转站的地址,而由于这些地址的地理位置差异,在不同的地方建造通讯中转站需要投入的成本也是不一样的,所幸在前期调查之后这些都是已知数据:建立第i个通讯中转站需要的成本为Pi(1≤i≤N)。另外公司调查得出了所有期望中的用户群,一共M个。关于第i个用户群的信息概括为Ai, Bi和Ci:这些用户会使用中转站Ai和中转站Bi进行通讯,公司可以获益Ci。(1≤i≤M, 1≤Ai, Bi≤N) THU集团的CS&T公司可以有选择的建立一些中转站(投入成本),为一些用户提供服务并获得收益(获益之和)。那么如何选择最终建立的中转站才能让公司的净获利最大呢?(净获利 = 获益之和 - 投入成本之和)
Input
输入文件中第一行有两个正整数N和M 。第二行中有N个整数描述每一个通讯中转站的建立成本,依次为P1, P2, …, PN 。以下M行,第(i + 2)行的三个数Ai, Bi和Ci描述第i个用户群的信息。所有变量的含义可以参见题目描述。
Output
你的程序只要向输出文件输出一个整数,表示公司可以得到的最大净获利。
Sample Input 1
5 5 1 2 3 4 5 1 2 3 2 3 4 1 3 3 1 4 2 4 5 3
Sample Output 1
4
Hint
【样例说明】选择建立1、2、3号中转站,则需要投入成本6,获利为10,因此得到最大收益4。【评分方法】本题没有部分分,你的程序的输出只有和我们的答案完全一致才能获得满分,否则不得分。【数据规模和约定】 80%的数据中:N≤200,M≤1 000。 100%的数据中:N≤5 000,M≤50 000,0≤Ci≤100,0≤Pi≤100。
Source
bzoj1497
最大点权子图题目
建立超级源点,超级汇点,源点与正点连接,流量为权值,汇点与负点连接,流量为权值的绝对值。
本来的边,权值为无穷大。
最后答案=正权点之和 - 最小割
如下图:最小割易知为9,这样建图,满足了要利润的话,两个点必须都选,不要就都不选了。
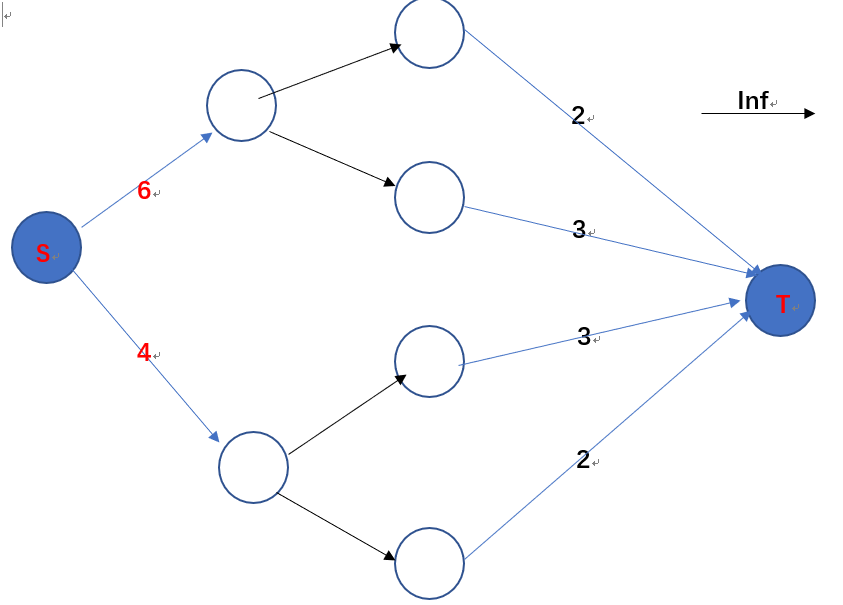
证明:推荐博客
1、最小割是关于s-t 的简单割 , 与s或t相连。
证:因为其他边都是INF
2、每一个简单割产生两个子图,记含有s点的是图S,含有t的是图T,则图S是闭合图
闭合图:选取的点构成的集合中任意一点连接的任意出弧,所指向的点也集合中
证:简单割中不含有边权为INF的边,即不含有连接S和T的边,也就是S和T不连通。
那么所有的边只能连接在图S之内
3、最小割产生的图S和图T,图S为最大权闭合子图
最大权闭合子图:在整个图中,权值和最大。
记:割集中,所有连接在s上的边的权值和为 x1 ,所有连接在t上的边的权值和为x2,那么割集中所有边权和为X=x1+x2;
记 图S中所有点的权值和为W,其中正权值和为w1,负权值和为 -w2. 所以W=w1-w2
而W+X=w1-w2+x1+x2; 其中w2=x2,因为 权值为负的点,必定连接到 t 上。
因而W+X=w1+x1;
显然X+x1为所有正点权之和,(图S中的+割集中的),记为SUM
故W=SUM - X。即 “图S中所有点的权值和“ = ”整个图的所有正权值之和“ - ”割集中所有边权之和“
因为SUM为定值,所以只要求最小割即可,这时图S的所有点的权值和最大,即最大权闭合子图。
1 #include<bits/stdc++.h> 2 using namespace std; 3 4 const int maxn=100010; 5 const int maxm=400010; 6 const int inf=0x3f3f3f3f; 7 struct Edge{ 8 int to,next,cap,flow,cost; 9 }edge[maxm]; 10 11 int tol; 12 int head[maxn]; 13 int gap[maxn],dep[maxn],cur[maxn]; 14 void init() { 15 tol=0; 16 memset(head,-1,sizeof(head)); 17 } 18 void addedge(int u,int v,int w,int rw=0) { 19 edge[tol].to=v;edge[tol].cap=w;edge[tol].flow=0; 20 edge[tol].next=head[u];head[u]=tol++; 21 edge[tol].to=u;edge[tol].cap=rw;edge[tol].flow=0; 22 edge[tol].next=head[v];head[v]=tol++; 23 } 24 25 int Q[maxn]; 26 void bfs(int start,int end) { 27 memset(dep,-1,sizeof(dep)); 28 memset(gap,0,sizeof(gap)); 29 gap[0]=1; 30 int front=0,rear=0; 31 dep[end]=0; 32 Q[rear++]=end; 33 while(front!=rear) { 34 int u=Q[front++]; 35 for(int i=head[u];i!=-1;i=edge[i].next) { 36 int v=edge[i].to; 37 if(dep[v]!=-1) continue; 38 Q[rear++]=v; 39 dep[v]=dep[u]+1; 40 gap[dep[v]]++; 41 } 42 } 43 } 44 45 int S[maxn]; 46 int sap(int start,int end,int n) { 47 bfs(start,end); 48 memcpy(cur,head,sizeof(head)); 49 int top=0; 50 int u=start; 51 int ans=0; 52 while(dep[start]<n) { 53 if(u==end) { 54 int minn=inf; 55 int inser; 56 for(int i=0;i<top;i++) { 57 if(minn>edge[S[i]].cap-edge[S[i]].flow) { 58 minn=edge[S[i]].cap-edge[S[i]].flow; 59 inser=i; 60 } 61 } 62 for(int i=0;i<top;i++) { 63 edge[S[i]].flow+=minn; 64 edge[S[i]^1].flow-=minn; 65 } 66 ans+=minn; 67 top=inser; 68 u=edge[S[top]^1].to; 69 continue; 70 } 71 bool flag=false; 72 int v; 73 for(int i=cur[u];i!=-1;i=edge[i].next) { 74 v=edge[i].to; 75 if(edge[i].cap-edge[i].flow&&dep[v]+1==dep[u]) { 76 flag=true; 77 cur[u]=i; 78 break; 79 } 80 } 81 if(flag) { 82 S[top++]=cur[u]; 83 u=v; 84 continue; 85 } 86 int minn=n; 87 for(int i=head[u];i!=-1;i=edge[i].next) { 88 if(edge[i].cap-edge[i].flow&&dep[edge[i].to]<minn) { 89 minn=dep[edge[i].to]; 90 cur[u]=i; 91 } 92 } 93 gap[dep[u]]--; 94 if(!gap[dep[u]]) return ans; 95 dep[u]=minn+1; 96 gap[dep[u]]++; 97 if(u!=start) u=edge[S[--top]^1].to; 98 } 99 return ans; 100 } 101 102 int n,m; 103 int main() { 104 while(~scanf("%d%d",&n,&m)) { 105 init(); 106 int s=0,t=n+m+1; 107 for(int i=1;i<=n;i++) { 108 int val; 109 scanf("%d",&val); 110 addedge(m+i,t,val); 111 } 112 int sum=0; 113 for(int i=1;i<=m;i++) { 114 int u,v,val; 115 scanf("%d%d%d",&u,&v,&val); 116 addedge(0,i,val); 117 addedge(i,m+u,inf); 118 addedge(i,m+v,inf); 119 sum+=val; 120 } 121 printf("%d\n",sum-sap(0,n+m+1,n+m+1)); 122 } 123 }



