Meet in the middle
搜索是\(OI\)中一个十分基础也十分重要的部分,近年来搜索题目越来越少,逐渐淡出人们的视野。但一些对搜索的优化,例如\(A\)*,迭代加深依旧会不时出现。本文讨论另一种搜索——折半搜索\((meet\ in\ the\ middle)\)。
由一道例题引入:CEOI2015 Day2 世界冰球锦标赛
我们可以用以下代码解决\(n\leq 20\)的数据,时间复杂度\(O(2^n)\)
void dfs(int step, int sum)
{
if (sum>m) return;
if (step==n+1) {ans++; return;}
dfs(step+1, sum+a[step]);
dfs(step+1, sum);
}
\(dfs\)有何弊端?
当搜索层数增加时,时间复杂度增加过快。
可不可以减少搜索层数,甚至降至一半?
当然可以。不然我这篇文章写什么
看网上两张很好的图就一目了然了。
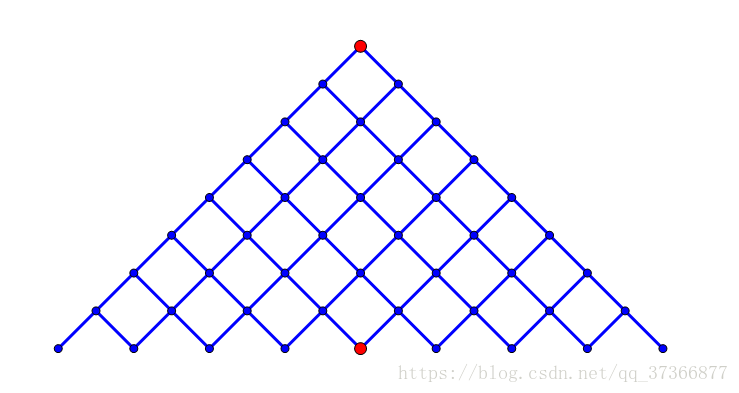

于是我们从\(1\)和\(n\)搜索\(\frac{n}{2}\)的深度,然后得到两个长为\(2^{\frac{n}{2}}\)的序列,对于第一个排序,然后用第二个在第一个中二分查找并统计答案即可。
(此代码不开\(O2\)在洛谷会\(T\)一个点,在\(loj\)跑的飞快,可能是满屏\(vector\)的缘故。)
#pragma GCC optimize (2)
#include<cstdio>
#include<vector>
#include<algorithm>
#define int long long
#define rep(i, a, b) for (register int i=(a); i<=(b); ++i)
#define per(i, a, b) for (register int i=(a); i>=(b); --i)
using namespace std;
const int N=45;
vector<int> a, b;
int c[N], m, ans, n, mid;
inline int read()
{
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
void dfs1(int step, int now)
{
if (now>m) return;
if (step>mid) {a.push_back(now); return;}
dfs1(step+1, now+c[step]);
dfs1(step+1, now);
}
void dfs2(int step, int now)
{
if (now>m) return;
if (step>n) {b.push_back(now); return;}
dfs2(step+1, now+c[step]);
dfs2(step+1, now);
}
signed main()
{
n=read(); m=read(); mid=n+1>>1;
rep(i, 1, n) c[i]=read();
dfs1(1, 0); dfs2(mid+1, 0);
sort(b.begin(), b.end());
for (int i:a) ans+=upper_bound(b.begin(), b.end(), m-i)-b.begin();
printf("%lld\n", ans);
return 0;
}
再来看另一道例题:USACO12OPEN 平衡的奶牛群
可以看看官方题解。
有一种显然的暴力,子集枚举即可, 时间复杂度\(O(3^n)\),无法通过。
我们把奶牛分为两组:黑色和白色。若\(S\)可行,那么\(S\)可被分为\(A,B\),使得\(sum_{A,black}-sum_{B,black}=sum_{B,white}-sum_{A,white}\)。于是我们可以计算黑色牛每一个子集可能的差值,白色同理。然后对于相同的差值进行配对,统计答案即可。
时间复杂度\(O(3^{\frac{n}{2}}\cdot 2^{\frac{n}{2}})\),即\(O((\sqrt{6})^n)\),可以通过。
依旧满屏\(vector\)
#include<cstdio>
#include<vector>
#include<algorithm>
#define rep(i, a, b) for (register int i=(a); i<=(b); ++i)
#define per(i, a, b) for (register int i=(a); i>=(b); --i)
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
vector<pair<int, int> > solve(vector<int> S)
{
vector<pair<int, int> > ans;
int n=S.size();
rep(i, 0, (1<<n)-1)
for (int j=i; ; j=(j-1)&i)
{
int sum=0;
rep(k, 0, n-1)
if (j&(1<<k)) sum-=S[k];
else if (i&(1<<k)) sum+=S[k];
if (sum>=0) ans.push_back(make_pair(sum, i));
if (!j) break;
}
sort(ans.begin(), ans.end());
ans.resize(unique(ans.begin(), ans.end())-ans.begin());
return ans;
}
int main()
{
int n=read();
vector<int> P, Q;
rep(i, 0, n-1)
{
int x=read();
if (i&1) P.push_back(x);
else Q.push_back(x);
}
vector<pair<int, int> > L=solve(P), R=solve(Q);
int p=0, q=0, l=L.size(), r=R.size();
vector<bool> vis(1<<n);
while (p<l && q<r)
{
if (L[p].first<R[q].first) p++;
else if (L[p].first>R[q].first) q++;
else
{
int p2=p, q2=q;
while (p2<l && L[p2].first==L[p].first) p2++;
while (q2<r && R[q2].first==R[q].first) q2++;
rep(i, p, p2-1) rep(j, q, q2-1)
vis[L[i].second|(R[j].second<<P.size())]=true,
p=p2; q=q2;
}
}
int ans=count(vis.begin()+1, vis.end(), true);
printf("%d\n", ans);
return 0;
}
即\(a*b+c=d*(e+f),d\neq 0\)。先枚举前三个,后三个枚举后二分查找即可。
#include<cstdio>
#include<vector>
#include<algorithm>
#define rep(i, a, b) for (register int i=(a); i<=(b); ++i)
#define per(i, a, b) for (register int i=(a); i>=(b); --i)
using namespace std;
vector<int> b, v, w;
int a[105], n; long long ans;
inline int read()
{
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
void prep()
{
rep(i, 1, n) rep(j, 1, n) rep(k, 1, n)
b.push_back(a[i]*a[j]+a[k]);
sort(b.begin(), b.end());
for (int i=0, j=0; i<b.size(); i=j+1, j++)
{
while (j<b.size()-1 && b[j+1]==b[i]) j++;
v.push_back(b[i]); w.push_back(j-i+1);
}
}
int check(int x)
{
int p=lower_bound(v.begin(), v.end(), x)-v.begin();
if (v[p]==x) return w[p]; else return 0;
}
void calc()
{
rep(i, 1, n) rep(j, 1, n) rep(k, 1, n)
if (a[i]) ans+=check((a[j]+a[k])*a[i]);
}
int main()
{
n=read();
rep(i, 1, n) a[i]=read();
prep(); calc();
printf("%lld\n", ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号