背包问题，P1282 多米诺骨牌

题目描述

多米诺骨牌由上下 22 个方块组成，每个方块中有 1∼61∼6 个点。现有排成行的上方块中点数之和记为 S1​，下方块中点数之和记为 S2​，它们的差为 ∣S1​−S2​∣。如图，S1=6+1+1+1=9，S2=1+5+3+2=11，∣S1​−S2​∣=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。请你计算最少旋转多少次才能使多米诺骨牌上下 22 行点数之差达到最小。

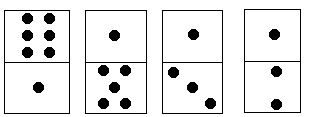
对于图中的例子，只要将最后一个多米诺骨牌旋转 180°180°，即可使上下 22 行点数之差为 00。

输入格式

输入文件的第一行是一个正整数 (1≤n≤1000)，表示多米诺骨牌数。接下来的 n 行表示 n 个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数 a 和 b，且 1≤a,b≤6。

输出格式

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

输入输出样例

输入 #1复制

4
6 1
1 5
1 3
1 2

输出 #1复制

1

这道题其实本质上是一个背包问题

更准确一点实际上使求最小开销的背包问题
体积为点数之差，开销为最小反转次数；

因此我们可以定义数组f[i][j]:表示前i的骨牌上下点数只差为j的最小反转次数

那么状态转移方程为f[i][j]=min(f[i-1][j-a[i]],f[i-1][j+a[i]]+1);

仔细观察上面这个状态转移方程，可以发现不能压缩成一维（但可以用滚动数组实现，这里就不写了）。
 

#include<iostream>
#include<set>
#include<vector>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#include<map>
#include<math.h>


using namespace std;
typedef long long LL;
const int N = 5000+2;
int f[1005][11005];
int a[1005], n;

int main() {
	cin >> n;
	for (int i = 1,t,k; i <= n; i++) {
		cin >> t >> k;
		a[i] = t - k;
	}
	memset(f, 0x3f3f3f3f, sizeof(f));
	f[0][N] = 0;
	for (int i = 1; i <= n; i++) {
		for (int j = -N; j<= N; j++) {
			f[i][j + N] = min(f[i - 1][j + N - a[i]], f[i - 1][j + N + a[i]] + 1);
		}
	}
	int ans = 0;
	for (int i = 0; i <= N; i++) {
		ans = min(f[n][i + N], f[n][-i + N]);
		//cout << ans << " ";
		if (ans <= 1000) {
			break;
		}
	}
	//cout << endl;
	cout << ans << endl;
	return 0;
}