LCA,模板题,P3379 【模板】最近公共祖先(LCA)
P3379 【模板】最近公共祖先(LCA) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目描述
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
输入格式
第一行包含三个正整数 N,M,S,分别表示树的结点个数、询问的个数和树根结点的序号。
接下来 N−1 行每行包含两个正整数 x,y,表示 x 结点和 y 结点之间有一条直接连接的边(数据保证可以构成树)。
接下来 M 行每行包含两个正整数 a,b,表示询问 a 结点和 b 结点的最近公共祖先。
输出格式
输出包含 M 行,每行包含一个正整数,依次为每一个询问的结果。
输入输出样例
输入 #1复制
5 5 4 3 1 2 4 5 1 1 4 2 4 3 2 3 5 1 2 4 5
输出 #1复制
4 4 1 4 4
说明/提示
对于 30%30% 的数据,N≤10,M≤10。
对于 70%70% 的数据,N≤10000,M≤10000。
对于 100%100% 的数据,1≤N,M≤500000,1≤x,y,a,b≤N,不保证 a不等于b。
样例说明:
该树结构如下:
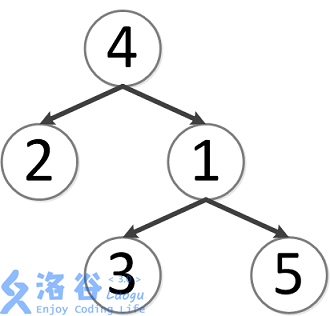
第一次询问:2,42,4 的最近公共祖先,故为 44。
第二次询问:3,23,2 的最近公共祖先,故为 44。
第三次询问:3,53,5 的最近公共祖先,故为 11。
第四次询问:1,21,2 的最近公共祖先,故为 44。
第五次询问:4,54,5 的最近公共祖先,故为 44。
故输出依次为 4,4,1,4,44,4,1,4,4。
2021/10/4 数据更新 @fstqwq:应要求加了两组数据卡掉了暴力跳。
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
const int N = 1e6 + 5, M = 5e5 + 5;
int n, m, s;
struct edge {
int to;
int next;
}edge[N];
int head[N];
int cnt;
int d[M],dp[M][20],v[M];
void add(int a, int b) {
edge[++cnt].to = b;
edge[cnt].next = head[a];
head[a] = cnt;
}
void dfs(int k) {
for (int i = 1; (1 << i) < d[k]; i++) {
dp[k][i] = dp[dp[k][i - 1]][i - 1];
}
for (int i = head[k]; i;i=edge[i].next) {
if (v[edge[i].to])
continue;
v[edge[i].to] = 1;
d[edge[i].to] = d[k] + 1;
dp[edge[i].to][0] = k;
dfs(edge[i].to);
}
}
int lca(int a, int b) {
if (d[a] < d[b])
swap(a, b);
int k = log2(d[a] - d[b]);
for (int i = k; i >= 0; i--) {
if (d[dp[a][i]] >= d[b])
a = dp[a][i];
}
k = log2(d[a]);
if (a == b)
return a;
for (int i = k; i >= 0; i--) {
if (dp[a][i] == dp[b][i])
continue;
a = dp[a][i];
b = dp[b][i];
}
return dp[a][0];
}
int main() {
scanf("%d%d%d", &n, &m, &s);
for (int i = 1,a,b; i < n; i++) {
scanf("%d%d", &a, &b);
add(a, b);
add(b, a);
}
d[s] = 1;
v[s] = 1;
dfs(s);
for (int i = 1,a,b; i <= m; i++) {
scanf("%d%d", &a, &b);
printf("%d\n", lca(a, b));
}
return 0;
}
 浙公网安备 33010602011771号
浙公网安备 33010602011771号