计算几何(一),ACM暑期培训
A - Cupid's Arrow
传说世上有一支丘比特的箭,凡是被这支箭射到的人,就会深深的爱上射箭的人。
世上无数人都曾经梦想得到这支箭。Lele当然也不例外。不过他想,在得到这支箭前,他总得先学会射箭。
日子一天天地过,Lele的箭术也越来越强,渐渐得,他不再满足于去射那圆形的靶子,他开始设计各种各样多边形的靶子。
不过,这样又出现了新的问题,由于长时间地练习射箭,Lele的视力已经高度近视,他现在甚至无法判断他的箭射到了靶子没有。所以他现在只能求助于聪明的Acmers,你能帮帮他嘛?
Input
本题目包含多组测试,请处理到文件结束。
在每组测试的第一行,包含一个正整数N(2<N<100),表示靶子的顶点数。
接着N行按顺时针方向给出这N个顶点的x和y坐标(0<x,y<1000)。
然后有一个正整数M,表示Lele射的箭的数目。
接下来M行分别给出Lele射的这些箭的X,Y坐标(0<X,Y<1000)。
Output
对于每枝箭,如果Lele射中了靶子,就在一行里面输出"Yes",否则输出"No"。
Sample
| Inputcopy | Outputcopy |
|---|---|
4 10 10 20 10 20 5 10 5 2 15 8 25 8 | Yes No |
解析:计算几何
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
const int N = 100 + 5;
const double eps = 1e-8;
const double PI = acos(-1.0);
typedef struct Point {
double x, y;
}Point;
Point p[N];
int n, m, num;
Point a, b, c, d;
int sign(double x) // 符号函数
{
if (fabs(x) < eps) return 0;
if (x < 0) return -1;
return 1;
}
double cross(double x, double y, double xx, double yy) {
return x * yy - y * xx;
}
bool online(Point a, Point b, Point c) {
if (fabs(cross(a.x - c.x, a.y - c.y, b.x - c.x, b.y - c.y)) < eps && a.x >= min(b.x, c.x) && a.x <= max(b.x, c.x) && a.y >= min(b.y, c.y) && a.y <= max(b.y, c.y))
return 1;
return 0;
}
int main() {
while (scanf("%d", &n) != EOF) {
for (int i = 1; i <= n; i++) {
scanf("%lf%lf", &p[i].x, &p[i].y);
}
scanf("%d", &m);
while (m--) {
num = 0;
scanf("%lf%lf", &a.x, &a.y);
b.x = -100, b.y = a.y;
int f = 0, js = 0;
for (int i = 1; i <= n; i++) {
c.x = p[i].x;
c.y = p[i].y;
if (i == n) {
d.x = p[1].x;
d.y = p[1].y;
}
else {
d.x = p[i + 1].x;
d.y = p[i + 1].y;
}
if (online(a, d, c)) {
f = 1;
break;
}
else {
if (c.y != d.y && a.y > min(c.y, d.y) && a.y <= max(c.y, d.y))
if (cross(a.x - d.x, a.y - d.y, c.x - d.x, c.y - d.y) * cross(b.x - d.x, b.y - d.y, c.x - d.x, c.y - d.y) < eps)
++js;
}
}
if (js & 1) f = 1;
if (f) printf("Yes\n");
else printf("No\n");
}
}
return 0;
}B - Lifting the Stone
There are many secret openings in the floor which are covered by a big heavy stone. When the stone is lifted up, a special mechanism detects this and activates poisoned arrows that are shot near the opening. The only possibility is to lift the stone very slowly and carefully. The ACM team must connect a rope to the stone and then lift it using a pulley. Moreover, the stone must be lifted all at once; no side can rise before another. So it is very important to find the centre of gravity and connect the rope exactly to that point. The stone has a polygonal shape and its height is the same throughout the whole polygonal area. Your task is to find the centre of gravity for the given polygon.
Input
The input consists of T test cases. The number of them (T) is given on the first line of the input file. Each test case begins with a line containing a single integer N (3 <= N <= 1000000) indicating the number of points that form the polygon. This is followed by N lines, each containing two integers Xi and Yi (|Xi|, |Yi| <= 20000). These numbers are the coordinates of the i-th point. When we connect the points in the given order, we get a polygon. You may assume that the edges never touch each other (except the neighboring ones) and that they never cross. The area of the polygon is never zero, i.e. it cannot collapse into a single line.
Output
Print exactly one line for each test case. The line should contain exactly two numbers separated by one space. These numbers are the coordinates of the centre of gravity. Round the coordinates to the nearest number with exactly two digits after the decimal point (0.005 rounds up to 0.01). Note that the centre of gravity may be outside the polygon, if its shape is not convex. If there is such a case in the input data, print the centre anyway.
Sample
| Inputcopy | Outputcopy |
|---|---|
2 4 5 0 0 5 -5 0 0 -5 4 1 1 11 1 11 11 1 11 | 0.00 0.00 6.00 6.00 |
解析:求多边形坐标
求解方法在这里
for (int i = 2; i < n; i++) {
area = ((1.0 * cross(p[i].x - p[1].x, p[i].y - p[1].y, p[i + 1].x - p[1].x, p[i + 1].y - p[1].y)) / 2);
sumarea += area;
sumx += area * (p[1].x + p[i].x + p[i + 1].x);
sumy += area * (p[1].y + p[i].y + p[i + 1].y);
//cout << sumx << " " << sumy << " " << sumarea<<endl;
}
具体的分析请看这位两位博主的博客:计算一个多边形的重心点坐标 - 简书 (jianshu.com)
(23条消息) 计算几何之多边形重心_cornivores的博客-CSDN博客
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
const int N = 1e6 + 5;
typedef struct Point {
double x, y;
}Point;
Point p[N];
int n;
double cross(double x, double y, double xx, double yy) {
//cout << x << " " << y << " " << xx << " " << yy << endl;
return x * yy - y * xx;
}
double ABS(double a) {
if (a < 0) {
return -a;
}
return a;
}
int main() {
int T;
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%lf%lf", &p[i].x, &p[i].y);
}
double sumx = 0, sumy = 0, area = 0, sumarea = 0;
for (int i = 2; i < n; i++) {
area = ((1.0 * cross(p[i].x - p[1].x, p[i].y - p[1].y, p[i + 1].x - p[1].x, p[i + 1].y - p[1].y)) / 2);
sumarea += area;
sumx += area * (p[1].x + p[i].x + p[i + 1].x);
sumy += area * (p[1].y + p[i].y + p[i + 1].y);
//cout << sumx << " " << sumy << " " << sumarea<<endl;
}
sumx /= 3 * sumarea;
sumy /= 3 * sumarea;
printf("%.2lf %.2lf\n", sumx, sumy);
}
}F - Space Ant
http://poj.org/problem?id=1696
The most exciting space discovery occurred at the end of the 20th century. In 1999, scientists traced down an ant-like creature in the planet Y1999 and called it M11. It has only one eye on the left side of its head and just three feet all on the right side of its body and suffers from three walking limitations:
- It can not turn right due to its special body structure.
- It leaves a red path while walking.
- It hates to pass over a previously red colored path, and never does that.
The pictures transmitted by the Discovery space ship depicts that plants in the Y1999 grow in special points on the planet. Analysis of several thousands of the pictures have resulted in discovering a magic coordinate system governing the grow points of the plants. In this coordinate system with x and y axes, no two plants share the same x or y.
An M11 needs to eat exactly one plant in each day to stay alive. When it eats one plant, it remains there for the rest of the day with no move. Next day, it looks for another plant to go there and eat it. If it can not reach any other plant it dies by the end of the day. Notice that it can reach a plant in any distance.
The problem is to find a path for an M11 to let it live longest.
Input is a set of (x, y) coordinates of plants. Suppose A with the coordinates (xA, yA) is the plant with the least y-coordinate. M11 starts from point (0,yA) heading towards plant A. Notice that the solution path should not cross itself and all of the turns should be counter-clockwise. Also note that the solution may visit more than two plants located on a same straight line.
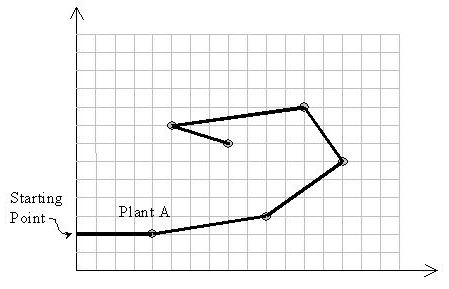
Input
The first line of the input is M, the number of test cases to be solved (1 <= M <= 10). For each test case, the first line is N, the number of plants in that test case (1 <= N <= 50), followed by N lines for each plant data. Each plant data consists of three integers: the first number is the unique plant index (1..N), followed by two positive integers x and y representing the coordinates of the plant. Plants are sorted by the increasing order on their indices in the input file. Suppose that the values of coordinates are at most 100.
Output
Output should have one separate line for the solution of each test case. A solution is the number of plants on the solution path, followed by the indices of visiting plants in the path in the order of their visits.
Sample
| Inputcopy | Outputcopy |
|---|---|
2 10 1 4 5 2 9 8 3 5 9 4 1 7 5 3 2 6 6 3 7 10 10 8 8 1 9 2 4 10 7 6 14 1 6 11 2 11 9 3 8 7 4 12 8 5 9 20 6 3 2 7 1 6 8 2 13 9 15 1 10 14 17 11 13 19 12 5 18 13 7 3 14 10 16 | 10 8 7 3 4 9 5 6 2 1 10 14 9 10 11 5 12 8 7 6 13 4 14 1 3 2 |
解析:极角坐标排序
这是一道典型的计较坐标排序的题目,但一开始我以为是求凸壳。
先找到题目要求的起点,然后对剩下的点进行极角排序,让极角最小的点作为起点,再对剩下的进行极角排序,一直迭代。
极角排序:利用叉积,看向量p1和p2的叉积(p1, p2)是否小于零,根据右手定则,是则说明p1在p2逆时针方向,即p1的极角比p2的大;极角相同则按离p0的距离升序排序。
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
const int maxn = 1e5 + 10;
struct Point {
int x, y, id;
}p[55];
int pos;
int cmp(const Point& a, const Point& b) {
return a.y < b.y;
}
int cross(int x, int y, int xx, int yy) {
return x * yy - y * xx;
}
int dis(Point p1, Point p2) {
return (p2.x - p1.x) * (p2.x - p1.x) + (p2.y - p1.y) * (p2.y - p1.y);
}
int cmpp(const Point& a, const Point& b) {
int t = cross(a.x - p[pos].x, a.y - p[pos].y, b.x - p[pos].x, b.y - p[pos].y);
if (t > 0)return 1;
else if (t == 0 && dis(p[pos], a) < dis(p[pos], b))return 1;
else
return 0;
}
int main() {
int T;
cin >> T;
while (T--) {
int n;
cin >> n;
Point p0;
p0.x = 0x3f3f3f3f;
p0.y = 0x3f3f3f3f;
for (int i = 1; i <= n; i++) {
scanf("%d%d%d", &p[i].id, &p[i].x, &p[i].y);
}
sort(p + 1, p + n + 1, cmp);
p[0].x = 0;
p[0].y = p[1].y;
vector<int>ans;
ans.push_back(p[1].id);
pos = 1;
for (int i = 2; i <= n; i++,pos++) {
sort(p + i, p + n + 1, cmpp);
ans.push_back(p[i].id);
}
cout << ans.size() << " ";
for (int i = 0; i < ans.size(); i++) {
cout << ans[i] << " ";
}
cout << endl;
}
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号