[Codeforces]906D Power Tower
虽说是一道裸题,但还是让小C学到了一点姿势的。
Description
给定一个长度为n的数组w,模数m和询问次数q,每次询问给定l,r,求:
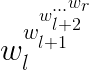
对m取模的值。
Input
第一行两个整数n,m,表示数组长度和模数。
接下来一行n个数,表示w数组。
接下来一行一个整数q,表示询问次数。
接下来q行,每行两个整数l,r,表示一次询问。
Output
对于每次询问,输出一行一个整数表示答案。
Sample Input
6 1000000000
1 2 2 3 3 3
8
1 1
1 6
2 2
2 3
2 4
4 4
4 5
4 6
Sample Output
1
1
2
4
256
3
27
597484987
HINT
1 ≤ n ≤ 105,1 ≤ m ≤ 109,1 ≤ wi ≤ 109,1 ≤ q ≤ 105,1 ≤ l ≤ r ≤ n。
Solution
看到这么清奇的式子,你大概会第一时间想到降幂大法吧?
先说说扩展欧拉定理,对于任意正整数a,b,p:
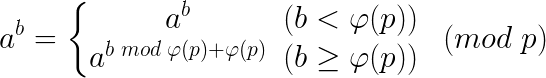
所以假设堆叠的幂次足够大,那么式子就可以转化为:


已知p经过至多2log次phi就会变成1。
所以递归求解,至多走到2log层模数就会变成1,所以返回0就行。
所以这道题就非常显然了,首先预处理出m的所有phi,对于每个询问,从l开始直接递归暴力,直到模数为1时返回。
还有一个问题,在求a^b%p的时候,怎么比较b和phi(p)的大小呢?
一种思路就是暴力计算a的后log项的值,注意还要特判1的情况,但这样写起来确实麻烦。
当然,有一种非常精妙的取模写法:
int modulo(ll x,int mod) {return x<mod?x:x%mod+mod;}
这是在做什么呢?这就是在比较b和phi(p)的大小,如果b<phi(p),返回b;否则返回b%phi(p)+phi(p)。
然后原式就变成了这样:

这样做看上去漏洞百出,可能的情况是,原本我们要计算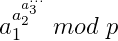 ,其中
,其中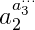 大等于
大等于 。
。
然而我们计算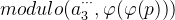 ,将
,将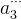 取模后,却发现
取模后,却发现 小于
小于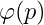 了。
了。
是否有这种可能呢?
其实就相当于判断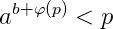 是否有可能成立,我们可以发现,当a>2时式子是不可能成立的。
是否有可能成立,我们可以发现,当a>2时式子是不可能成立的。
所以我们来看一看 是否有可能成立。
是否有可能成立。
有可能。
当且仅当p=6时,不等式成立。
然而6有什么特殊的性质呢?
我们发现phi(x)=6只有三个解:x=7,x=9或x=18。
所以接下来我们只要证明 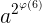 和
和 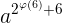 即
即 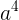 和
和 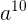 在对x取模的意义下相等即可。(其中phi(x)=6)
在对x取模的意义下相等即可。(其中phi(x)=6)
若a为x的倍数,显然它们对x取模都等于0,对于答案无影响。
当x=7时, ,所以
,所以 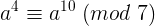 ;
;
当x=9时,若 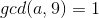 ,则影响同上;
,则影响同上;
若 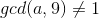 ,一定有
,一定有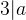 ,所以一定有
,所以一定有  ,
,
所以一定有 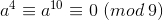 ,对于答案是没有影响的;
,对于答案是没有影响的;
当x=18时,若 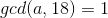 或
或 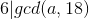 ,则影响同上;
,则影响同上;
我们有一个显然的结论:同余方程 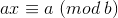 的解为
的解为 
若 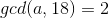 ,则
,则 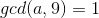 ,则
,则  ,则
,则 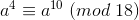
若 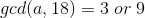 ,则
,则  且
且 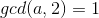 ,则
,则 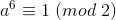 ,则
,则 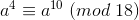
所以综上,我们就证明了该算法的正确性。
时间复杂度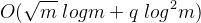 。
。
#include <cstdio> #include <cstring> #include <algorithm> #define ll long long #define MN 100005 using namespace std; int a[MN],mod[MN]; int n,p; bool fg; inline int read() { int n=0,f=1; char c=getchar(); while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();} while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();} return n*f; } inline int pro(ll x,int md) {return x<md?x:x%md+md;} inline int mi(int x,int y,int md) { register int z=1; for (;y;x=pro(1LL*x*x,md),y>>=1) if (y&1) z=pro(1LL*z*x,md); return z; } int dfs(int x,int y,int lim) { if (x==lim) return a[x]>=mod[y]?a[x]%mod[y]+mod[y]:a[x]; if (mod[y]==1) return 1; return mi(a[x],dfs(x+1,y+1,lim),mod[y]); } int main() { register int i,j,x,y; n=read(); mod[1]=read(); for (i=1;mod[i]>1;++i) { mod[i+1]=x=mod[i]; for (j=2;j*j<=x;++j) { for (fg=0;x%j==0;x/=j,fg=true); if (fg) mod[i+1]=1LL*mod[i+1]*(j-1)/j; } if (x>1) mod[i+1]=1LL*mod[i+1]*(x-1)/x; } for (i=1;i<=n;++i) a[i]=read(); for (p=read();p;--p) { x=read(); y=read(); printf("%d\n",dfs(x,1,y)%mod[1]); } }
Last Word
打Codeforces的时候正纳闷这种情况该怎么处理,却发现大佬们清一色都是这么写的。
小C觉得自己的证明蠢得不行啊……
如果读者有更直观的证明该算法的正确性的方法请务必告诉小C。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号