关于快速沃尔什变换(FWT)的一点学习和思考
最近在学FWT，抽点时间出来把这个算法总结一下。
快速沃尔什变换（Fast Walsh-Hadamard Transform），简称FWT。是快速完成集合卷积运算的一种算法。
主要功能是求：
，其中
为集合运算符。
就像FFT一样，FWT是对数组的一种变换，我们称数组X的变换为FWT(X)。
所以FWT的核心思想是：
为了求得C=A★B，我们瞎搞搞出一个变换FWT(X)，
使得FWT(C)=FWT(A) 
FWT(B)，然后根据FWT(C)求得C。
（其中★表示卷积运算，
表示将数组对应下标的数相乘的运算）
也就是说我们可以通过FWT(X)变换把复杂度O(n^2)的★运算变为O(n)的
运算。
跟FFT是完全相同的。所以我们考虑怎么搞出这个FWT(X)。
与运算(&)和或运算(|)最容易理解，我们先讲讲这两个怎么搞。我们以或运算为例。
若 x | y = z，那么x和y一定满足二进制中的1为z的子集。
所以我们可以令FWT(A)=A'，其中
。（“i | j = i”就是表示“j满足二进制中的1为i的子集”）
（虽然以上两行根本构不成逻辑，但是请相信这个定义就是正确的）
于是我们就有C'=A' 
B'，从这些数组的定义来看，这个式子确实是正确的。
然后我们就要研究一下FWT(A)也就是A'怎么求。当然不能枚举 i 的子集，这样复杂度太高。
既然是二进制的，我们不妨考虑用分治进行计算。（为毛是二进制就要用分治啊喂！）
我们设A0为A的前一半，A1为A的后一半，如果A的长度为2^k，那么A0、A1的长度为2^(k-1)。
如果我们知道了FWT(A0)和FWT(A1)，那么FWT(A)是不是就可以求了呢？当然可以。
FWT(A)的前一半相当于二进制位的第k位填了0，那么是它子集的仍然只有FWT(A0) （它本身）；
FWT(A)的后一半相当于二进制位的第k位填了1，那么是它子集的不仅仅有FWT(A1) （它本身），还有FWT(A0)。
那么转移就出来了，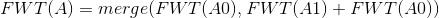
。
其中merge(X,Y)为X和Y两个数组接在一起， 
表示将数组对应下标的数相加的运算。
这样我们就在O(2^k*k)也就是O(nlogn)的时间内求出了FWT(A)。
还有一个问题，我们怎么通过FWT(C)求得C？
这不就是FWT()的逆变换吗？根据转移方程，你难道不会倒着推回来吗？
这其实就相当于你知道了A0'、A1'，然后要求得A0、A1。
因为我们已经知道了A0'=A0，A1'=A1+A0，所以我们就有A0=A0'，A1=A1'-A0'。
所以：
。
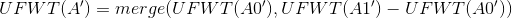既然知道了或运算，与运算也是一样的，因为与运算和或运算本质是相同的。
读者可以试着自己推一遍，再继续往下看：
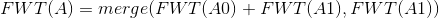
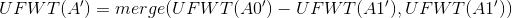
然后就是鬼畜的异或，先说结论：
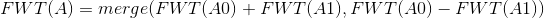
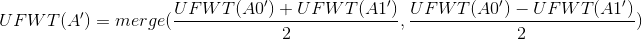
一种比较靠谱的说法是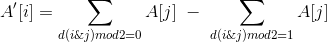
，其中d(x)为x的二进制中1的个数。
先想一想再往下看吧~
然后你可能会想，与和或本质上不是相同的吗？
然后就有
，其中d'(x)为x的二进制（到第k位为止）中0的个数。
然后就有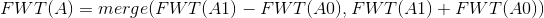
，
。
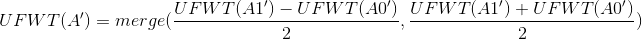然后结果是一毛一样的。
（其实就是把整个数组倒过来而已）
所以又回到FWT的核心思想：
为了求得C=A★B，我们瞎搞搞出一个变换FWT(X)，
使得FWT(C)=FWT(A) FWT(B)，然后根据FWT(C)求得C。
所以我们只要找到运算中，数字x的一个特征FWT(x)，满足FWT(x y)=FWT(x)*FWT(y)。这个特征就是FWT啦~
怎么样，是不是给你一种“我上我也行”的感觉？
然后你试图寻求异或FWT的更简单的公式：
然后你开始脑补：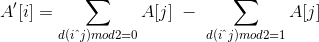
。
然后惊喜地发现正好满足 FWT(C)=FWT(A) FWT(B) ！
然后你开始写转移公式：
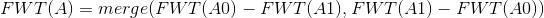
（以上18行都是小C在口胡）
到底有没有靠谱的做法呢？小D说他有一种解方程的做法。
为了不失一般性，假设A、B、C数组的长度为2。C=A★B，为异或卷积运算。
然后显然C[0] = A[0]*B[0] + A[1]*B[1] ， C[1] = A[0]*B[1] + A[1]*B[0]。
然后我们开始变形了！由于(我们猜想)FWT(A)一定是a*FWT(A0) + b*FWT(A1)的形式，所以：
设A'[0] = a*A[0] + b*A[1]，A'[1] = c*A[0] + d*A[1]。
B和C同理，因为小C知道列一大堆方程出来肯定没人看所以小C就不列出来了。
然后就有C'[0] = A'[0]*B'[0]。解方程，得：
因为a,b不同时等于0，所以a=1，b=±1。同理，c=1，d=±1。
（由于解方程过程中有很多槽点所以小C也不能保证正确性）
然后究竟是+1还是-1呢？小D给的说法是“枚举，check一下”。
check个鬼啊(╯‵□′)╯︵┻━┻！这个做法槽点真的太多了好吗？
不过能够得出正确答案是真的。
