[Codeforces]871D Paths

　　失踪OJ回归。

　　毕竟这样的数论没做过几道，碰上一些具体的应用还是无所适从啊。小C还是借助这题大致摸索一下莫比乌斯函数吧。

 

Description

　　有n个点，标号为1~n，为这n个点建一张无向图。两个点x,y之间有连边当且仅当x,y不互质，求两两点对之间的最短路d(x,y)(1<=x<y<=n)之和。（如果两个点不连通，令它们之间的最短路为0）

Input

　　只有一行，一个正整数n。

Output

　　输出两两点对之间的最短路之和。

Sample Input

　　10

Sample Output

　　44

HINT

　　1<=n<=10^7。

 

Solution

　　通过仔细思考，1对答案没有贡献，我们不考虑1。设low[x]为x的最小质因数，我们可以把点对(x,y)之间的关系分为四种：

　　①gcd(x,y)>1：d(x,y)=1；

　　②gcd(x,y)=1且low[x]*low[y]<=n：d(x,y)=d(x,low[x]*low[y])+d(low[x]*low[y],y)=2；

　　③gcd(x,y)=1且low[x]*low[y]>n且low[x]*2<=n且low[y]*2<=n：d(x,y)=d(x,low[x]*2)+d(low[x]*2,low[y]*2)+d(low[y]*2,y)=3；

　　④gcd(x,y)=1且low[x]*2>n或low[y]*2>n：d(x,y)=0。

　　其中第一种和第四种都很好处理，第一种用欧拉函数，第四种求出每个数的最小质因数，统计一下low[x]>n/2的个数计算即可。

　　用所有方案数减去第一种和第四种的方案数就是第二和第三种的方案数和。

　　接下来的任务，就是求出第二种或第三种其中一种情况的方案数即可。第二种似乎看起来比第三种好求。

　　很自然地，我们想到对于每个low[x]统计x的个数。因此对于每个low[x]用二分或指针法加上前缀和就可以分别计算答案。

　　然而这个统计方法显然是有重复的。因为这样把gcd不为1的对数也算进去了，且每对这样的x,y恰好被算了一次。

　　所以现在我们要统计的是：gcd(x,y)>1且low[x]*low[y]<=n的x,y对数。

　　所以我们似乎可以枚举gcd(x,y)，统计这样的x,y对数？但显然枚举gcd太难受了，枚举公因数还是更容易一些。

　　所以每对满足gcd(x,y)>1的x,y被算了 gcd(x,y)的因数个数 次！

　　怎么才能让每对满足x,y被算了 gcd(x,y)的因数个数 次后相当于只被算了一次呢？容斥？怎么容斥？

　　然后我们就想到了莫比乌斯反演中的，

　　由于我们并没有考虑1，因此，正好就是我们所想要求的啊！

　　所以现在我们求的是。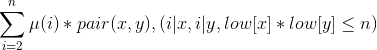

　　我们枚举i，对于每个i考虑怎么计算x,y的对数。

　　当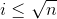时，low[x]*low[y]无论如何都不会大于n，所以这样的x,y对数为(n/i)*(n/i)。

　　当时，low[x]*low[y]只有当x=y=i且i为质数的时候才会大于n，当满足这种情况时减去1即可。

　　所以我们就完成了这漫长的计算，时间复杂度O(n)。

#include <algorithm>
#include <cstring>
#include <cstdio>
#define ll long long
#define MN 10000005
using namespace std;
int n,prin,dys;
int zx[MN],pri[MN],phi[MN],miu[MN],sm[MN];
ll ans,sum;

inline int read()
{
    int n=0,f=1; char c=getchar();
    while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();}
    while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();}
    return n*f;
}

int main()
{
    register int i,j;
    n=read();
    for (phi[1]=miu[1]=1,i=2;i<=n;++i)
    {
        if (!zx[i]) pri[++prin]=i,zx[i]=prin,phi[i]=i-1,miu[i]=-1;
        for (j=1;i*pri[j]<=n;++j)
        {
            zx[i*pri[j]]=j;
            if (i%pri[j]==0) {phi[i*pri[j]]=phi[i]*pri[j]; miu[i*pri[j]]=0; break;}
            else {phi[i*pri[j]]=phi[i]*(pri[j]-1); miu[i*pri[j]]=-miu[i];}
        }
        ans+=i-phi[i]-1; ++sm[zx[i]];
    }
    for (i=1;i<=prin;++i) if (pri[i]*2>n) ++dys;
    ans+=(1LL*(n-1)*(n-2)/2-ans-1LL*dys*(n-dys-1)-1LL*dys*(dys-1)/2)*3;
    for (i=1;i<=prin;++i) sm[i]+=sm[i-1];
    for (i=1,j=prin;i<=prin;++i)
    {
        for (;j&&pri[i]*pri[j]>n;--j);
        sum+=1LL*sm[j]*(sm[i]-sm[i-1]);
    }
    for (i=2;i<=n;++i) sum+=(1LL*(n/i)*(n/i)-(pri[zx[i]]==i&&1LL*i*i>n))*miu[i];
    printf("%I64d",ans-sum/2);
}

 

Last Word

　　这其中的计算思路还真是令人捉摸不透啊，各个计算之间的关联度很小，很显然需要很多碎片化的思路拼接起来才能完成这道题。

　　莫比乌斯函数其实就是通过枚举因数来进行的容斥吧。