[BZOJ]3672 购票(Noi2014)

　　革命尚未成功，同志还需努力。

 

Description

　　今年夏天，NOI在SZ市迎来了她30周岁的生日。来自全国 n 个城市的OIer们都会从各地出发，到SZ市参加这次盛会。

　　全国的城市构成了一棵以SZ市为根的有根树，每个城市与它的父亲用道路连接。为了方便起见，我们将全国的 n 个城市用 1 到 n 的整数编号。其中SZ市的编号为 1。对于除SZ市之外的任意一个城市 v，我们给出了它在这棵树上的父亲城市 f_v  以及到父亲城市道路的长度 s_v。

　　从城市 v 前往SZ市的方法为：选择城市 v 的一个祖先 a，支付购票的费用，乘坐交通工具到达 a。再选择城市 a 的一个祖先 b，支付费用并到达 b。以此类推，直至到达SZ市。

　　对于任意一个城市 v，我们会给出一个交通工具的距离限制 l_v。对于城市 v 的祖先 a，只有当它们之间所有道路的总长度不超过 l_v  时，从城市 v 才可以通过一次购票到达城市 a，否则不能通过一次购票到达。对于每个城市 v，我们还会给出两个非负整数 p_v,q_v  作为票价参数。若城市 v 到城市 a 所有道路的总长度为 d，那么从城市 v 到城市 a 购买的票价为 dp_v+q_v。

　　每个城市的OIer都希望自己到达SZ市时，用于购票的总资金最少。你的任务就是，告诉每个城市的OIer他们所花的最少资金是多少。

Input

　　第 1 行包含2个非负整数 n,t，分别表示城市的个数和数据类型（其意义将在后面提到）。
　　输入文件的第 2 到 n 行，每行描述一个除SZ之外的城市。其中第 v 行包含 5 个非负整数 f_v,s_v,p_v,q_v,l_v，分别表示城市 v 的父亲城市，它到父亲城市道路的长度，票价的两个参数和距离限制。
　　请注意：输入不包含编号为 1 的SZ市，第 2 行到第 n 行分别描述的是城市 2 到城市 n。

Output

　　输出包含 n-1 行，每行包含一个整数。其中第 v 行表示从城市 v+1 出发，到达SZ市最少的购票费用。同样请注意：输出不包含编号为 1 的SZ市。

Sample Input

　　7 3
　　1 2 20 0 3
　　1 5 10 100 5
　　2 4 10 10 10
　　2 9 1 100 10
　　3 5 20 100 10
　　4 4 20 0 10

Sample Output

　　40
　　150
　　70
　　149
　　300
　　150

HINT

　　对于所有测试数据，保证 0≤p_v≤10⁶，0≤q_v≤10¹²，1≤f_v<v；保证 0<s_v≤l_v≤2×10¹¹，且任意城市到SZ市的总路程长度不超过 2×10¹¹。
　　输入的 t 表示数据类型，0≤t<4，其中：
　　当 t=0 或 2 时，对输入的所有城市 v，都有 f_v=v-1，即所有城市构成一个以SZ市为终点的链；
　　当 t=0 或 1 时，对输入的所有城市 v，都有 l_v=2×10^11，即没有移动的距离限制，每个城市都能到达它的所有祖先；
　　当 t=3 时，数据没有特殊性质。
　　n=2×10^5。

 

Solution

　　看上去觉得可做系列。

　　首先很容易写出答案的DP转移方程：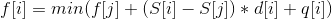

　　设S[x]为节点x到根的距离，其中j满足j为i的祖先且S[i]-S[j]<=l[i]。

　　既然是一个1D-1D的方程，我们暂时考虑斜率优化的做法。

　　经过数学推导，得到不等式。当j为k的祖先时，若从j转移至i比从k转移更优，则有

　　　　

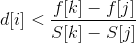
　　所以就相当于让每一个可以转移到点i的节点j，对应平面上的一个点(S[j],f[j])，我们要找到一个点x满足：

　　　　对于每一个点y为x的祖先，都有；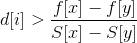

　　　　对于每一个点y为x的子孙，都有；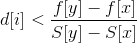

　　如下图，红线的斜率为d[i]，则从编号为x的点转移最优。

　　　　

　　其实最优转移点就是红线从右下角扫描过来时第一个碰到的点。

　　于是我们发现第一个碰到的点肯定位于这些点的凸包上，所以我们只要求出凸包，将斜率在凸包上二分找最优转移点即可。

　　由于红线的斜率即d[i]为自然数，我们只需维护半边凸包。

　　　　

　　所以，我们只要得到一段区间上的凸包，就能得到答案，我们选择大力树套树维护凸包。

　　（用线段树的的每一个节点表示从当前点到根节点的链上 该线段树的节点所表示的区间上 的凸包）

　　由于是在一棵树上进行维护，所以从当前点到根节点的链（其实是一个栈）是会改变的，有进栈和出栈操作。

　　由于有出栈操作，可持久化显然会MLE，我们就必须支持撤销操作。

　　小C写的是zkw线段树套线段树，当然还有更优更简单的zkw套无旋Treap做法。（小C作死后面会提到）

 

　　无旋Treap就是每次存下split掉的那 logn 棵树（的根），撤销时merge回来即可。

　　线段树就是每次存下每次（最多logn次）删掉的那个节点的右子树的编号，撤销时补回来即可。（如下图）（空间复杂度预警）

　　　

　　如果更新凸包时，新的节点插入于红色框处，那么绿色框就要被删去，即将其父亲的右儿子指向0即可。

　　线段树需要动态开点，这样通过数学推导，空间只有O(nlogn)。

　　每棵线段树的根节点的范围还要根据 zkw线段树的节点 对应的区间的宽度 来定，否则会被卡常。

　　（读者：TMD线段树要注意的东西那么多还不如不说。 小C：人家打了好久的就是要说你来打我啊）

　　总时间复杂度。

 

　　这题似乎还有很巧妙的cdq分治算法。

　　每次像点分治那样做，然后用包含根的那个子树更新其它子树。

　　　　

　　如图，红色点为重心，用绿色链来更新黄色部分子树的答案。

　　将每个黄色部分内的点按照能爬到绿色链内的深度排序，将绿色链内依次加入凸包时就可以顺便更新答案了……你懂的。

　　对于每一个分治结构都这样做，总复杂度O(nlogn)。

#include <cstdio>
#include <algorithm>
#define l(a) (son[a][0])
#define r(a) (son[a][1])
#define ll long long
#define INF 1LL<<62
#define MM 7400005
#define MN 200005
#define MS 19
using namespace std;
struct node
{
    int pos; double slope;
    friend node operator+(const node& a,const node& b){return b.pos?b:(node){0,0};}
}t[MM],g[MN][MS];
struct edge{int nex,to; ll wt;}e[MN];
int pin,din,n,tp,MO;
int hr[MN],a[MN],rt[MN*3],st[MN],son[MM][2];
int cg[MN][MS][MS],bh[MN][MS];
ll f[MN],s[MN],lim[MN],b[MN];

inline ll read()
{
    ll n=0,f=1; char c=getchar();
    while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();}
    while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();}
    return n*f;
}
inline void ins(int x,int y,ll z) {e[++pin]=(edge){hr[x],y,z}; hr[x]=pin;}

node Tgetans(int x,int L,int R,int z)
{
    if (!x||L==R) return (node){0,0};
    int mid=L+R>>1;
    if (!t[l(x)].pos||z<t[l(x)].slope) return Tgetans(l(x),L,mid,z);
    else {node lt=Tgetans(r(x),mid+1,R,z); return lt.pos?lt:t[l(x)];}
}
void Tmodify(int& x,int L,int R,int y,int z,int pre,int depth)
{
    if (!x) x=++din;
    if (L==R) {g[y][z]=t[x]; bh[y][z]=L; t[x]=(node){y,pre?(double)(f[y]-f[pre])/(s[y]-s[pre]):0}; return;}
    int mid=L+R>>1;
    if (t[l(x)].pos&&(double)(f[y]-f[t[l(x)].pos])/(s[y]-s[t[l(x)].pos])>t[l(x)].slope) Tmodify(r(x),mid+1,R,y,z,t[l(x)].pos,depth+1);
    else {Tmodify(l(x),L,mid,y,z,pre,depth+1); cg[y][z][depth]=r(x); r(x)=0;}
    t[x]=t[l(x)]+t[r(x)];
}
void Tcance(int x,int L,int R,int y,int z,int depth)
{
    if (L==R) {t[x]=g[y][z]; return;}
    int mid=L+R>>1;
    if (bh[y][z]>mid) Tcance(r(x),mid+1,R,y,z,depth+1);
    else {Tcance(l(x),L,mid,y,z,depth+1); r(x)=cg[y][z][depth];}
    t[x]=t[l(x)]+t[r(x)];
}

void getans(int x,int ql,int qr,int z)
{
    node lt; f[x]=INF;
    register int j;
    for (j=1,ql+=MO,qr+=MO;ql<=qr;ql>>=1,qr>>=1,j<<=1)
    {
        if ( ql&1)
        {
            if (t[rt[ql]].pos&&z>=t[rt[ql]].slope) lt=t[rt[ql++]];
            else lt=Tgetans(rt[ql++],1,j,z);
            f[x]=min(f[x],f[lt.pos]+(s[x]-s[lt.pos])*z+b[x]);
        }
        if (~qr&1)
        {
            if (t[rt[qr]].pos&&z>=t[rt[qr]].slope) lt=t[rt[qr--]];
            else lt=Tgetans(rt[qr--],1,j,z);
            f[x]=min(f[x],f[lt.pos]+(s[x]-s[lt.pos])*z+b[x]);
        }
    }
}
void modify(int x,int q)
{
    register int i,j;
    for (i=0,j=1,q+=MO;q;q>>=1,++i,j<<=1) Tmodify(rt[q],1,j,x,i,0,0);
}
void cance(int x,int q)
{
    register int i,j;
    for (i=0,j=1,q+=MO;q;q>>=1,++i,j<<=1) Tcance(rt[q],1,j,x,i,0);
}

void dfs(int x)
{
    register int i,L,R;
    for (L=1,R=tp;L<R;)
    {
        int mid=L+R>>1;
        if (s[x]-s[st[mid]]>lim[x]) L=mid+1; else R=mid;
    }
    if (R) getans(x,R,tp,a[x]);
    st[++tp]=x; modify(x,tp);
    for (i=hr[x];i;i=e[i].nex)
    {
        s[e[i].to]=s[x]+e[i].wt;
        dfs(e[i].to);
    }
    cance(x,tp); --tp;
}


int main()
{
    register int i,x;
    register ll y;
    n=read(); x=read();
    for (MO=1;MO<n;MO<<=1); --MO;
    for (i=2;i<=n;++i)
    {
        x=read(); y=read(); ins(x,i,y);
        a[i]=read(); b[i]=read(); lim[i]=read();
    }
    dfs(1);
    for (i=2;i<=n;++i) printf("%lld\n",f[i]);
}

 

Last Word

　　这大概是小C唯一一次那么执着地要把一种自己想的做法写完的题目了。（没办法小C强迫症）

　　刚开始看到题目时忽略了有距离限制的条件，果断就打了线段树维护凸包上去，结果打完才发现GG。

　　看错题面癌持续发作的小C之后又卯足劲向南墙撞去……至于写了什么丢人的代码这里就不说了。

　　最后发现要求出区间凸包只有树套树一条路，线段树套平衡树的做法很显然……

　　但小C觉得既然只是维护一个栈，就只有修改一个点和删除一个后缀的操作，线段树似乎也可以完成？

　　于是抱着尝试的心态写了个可持久化线段树，发现MLE之后，小C才真真正正地被恶心到了。

　　然后就写了撤销操作，通过计算发现动态开点空间十分科学。然后交上去跑了3.5秒TLE……Excuse me？

　　仔细想想只有zkw的1号节点才要开[1,n]，而2、3号节点只要开[1,n/2]？

　　然后就过了……小C作个死还这么难啊……

　　发现小C写的zkw跟《统计的力量》里面写的有些不同诶，人家是开区间而小C是闭区间。

　　最后小D太强啦，本一线上清华啦，orz ditoly。