POJ 1375 Intervals (圆的切线)
Intervals
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 4116 | Accepted: 1216 |
Description
In the ceiling in the basement of a newly open developers building a light source has been installed. Unfortunately, the material used to cover the floor is very sensitive to light. It turned out that its expected life time is decreasing dramatically. To avoid this, authorities have decided to protect light sensitive areas from strong light by covering them. The solution was not very easy because, as it is common, in the basement there are different pipelines under the ceiling and the authorities want to install the covers just on those parts of the floor that are not shielded from the light by pipes. To cope with the situation, the first decision was to simplify the real situation and, instead of solving the problem in 3D space, to construct a 2D model first.
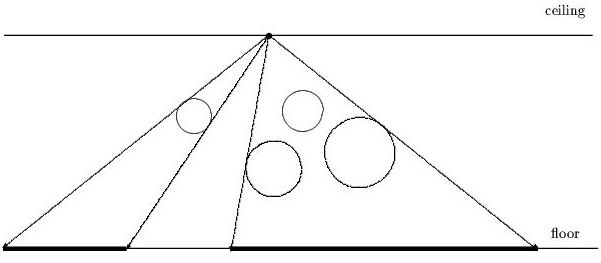
Within this model, the x-axis has been aligned with the level of the floor. The light is considered to be a point light source with integer co-ordinates [bx,by]. The pipes are represented by circles. The center of the circle i has the integer co-ordinates [cxi,cyi] and an integer radius ri. As pipes are made from solid material, circles cannot overlap. Pipes cannot reflect the light and the light cannot go through the pipes. You have to write a program which will determine the non-overlapping intervals on the x-axis where there is, due to the pipes, no light from the light source.
![]()
Within this model, the x-axis has been aligned with the level of the floor. The light is considered to be a point light source with integer co-ordinates [bx,by]. The pipes are represented by circles. The center of the circle i has the integer co-ordinates [cxi,cyi] and an integer radius ri. As pipes are made from solid material, circles cannot overlap. Pipes cannot reflect the light and the light cannot go through the pipes. You have to write a program which will determine the non-overlapping intervals on the x-axis where there is, due to the pipes, no light from the light source.
Input
The input consists of blocks of lines, each of which except the last describes one situation in the basement. The first line of each block contains a positive integer number N < 500 expressing the number of pipes. The second line of the block contains two integers bx and by separated by one space. Each of the next N lines of the block contains integers cxi, cyi and ri, where cyi + ri < by. Integers in individual lines are separated by one space. The last block consists of one line containing n = 0.
Output
The output consists of blocks of lines, corresponding to the blocks in the input(except the last one). One empty line must be put after each block in the output. Each of the individual lines of the blocks in the output will contain two real numbers, the endpoints of the interval where there is no light from the given point light source. The reals are exact to two decimal places and separated by one space. The intervals are sorted according to increasing x-coordinate.
Sample Input
6
300 450
70 50 30
120 20 20
270 40 10
250 85 20
220 30 30
380 100 100
1
300 300
300 150 90
1
300 300
390 150 90
0
Sample Output
0.72 78.86
88.50 133.94
181.04 549.93
75.00 525.00
300.00 862.50
Source
题意: 给出一个光源,给出一些圆,求投影区间。
思路:求点对于各个圆的切线,最后更新就行了。

代码:

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 505;
const double EP = 1e-9;
const double PI = acos( -1.0 );
struct POINT
{
double x;
double y;
POINT(double a=0, double b=0)
{
x=a; //constructor
y=b;
}
} s,q;
double dist(POINT p1,POINT p2) // 返回两点之间欧氏距离
{
return( sqrt( (p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y) ) );
}
int sgn(double x)
{
if(fabs(x) < EP)return 0;
if(x < 0)return -1;
else return 1;
}
//调整到0~2*PI区间
double fix( double ang )
{
while ( sgn( ang ) < 0 ) ang += 2.0*PI;
while ( sgn( ang - PI - PI ) >= 0 ) ang -= 2.0*PI;
return ang;
}
struct node
{
double l,r;
}line[N];
bool cmp(node a,node b)
{
return a.l<b.l;
}
int main()
{
int n;
double r;
while(~scanf("%d",&n)&&n)
{
scanf("%lf%lf",&s.x,&s.y);
for(int i=0; i<n; i++)
{
scanf("%lf%lf%lf",&q.x,&q.y,&r);
double d = dist(s,q);
double a = asin(r/d),b = asin((s.x-q.x)/d);
double ang1 = fix(a+b), ang2 = fix(b-a);
line[i].l = s.x-s.y*tan(ang1);
line[i].r = s.x-s.y*tan(ang2);
}
sort(line,line+n,cmp);
double L = line[0].l, R = line[0].r;
for(int i=0; i<n; i++)
{
if(line[i].l > R)
{
printf("%.2f %.2f\n",L,R);
L = line[i].l, R = line[i].r;
}
else
{
R = max(R,line[i].r);
}
}
printf("%.2f %.2f\n\n",L,R);
}
return 0;
}
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 505;
const double EP = 1e-9;
const double PI = acos( -1.0 );
struct POINT
{
double x;
double y;
POINT(double a=0, double b=0)
{
x=a; //constructor
y=b;
}
} s,q;
double dist(POINT p1,POINT p2) // 返回两点之间欧氏距离
{
return( sqrt( (p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y) ) );
}
int sgn(double x)
{
if(fabs(x) < EP)return 0;
if(x < 0)return -1;
else return 1;
}
//调整到0~2*PI区间
double fix( double ang )
{
while ( sgn( ang ) < 0 ) ang += 2.0*PI;
while ( sgn( ang - PI - PI ) >= 0 ) ang -= 2.0*PI;
return ang;
}
struct node
{
double l,r;
}line[N];
bool cmp(node a,node b)
{
return a.l<b.l;
}
int main()
{
int n;
double r;
while(~scanf("%d",&n)&&n)
{
scanf("%lf%lf",&s.x,&s.y);
for(int i=0; i<n; i++)
{
scanf("%lf%lf%lf",&q.x,&q.y,&r);
double d = dist(s,q);
double a = asin(r/d),b = asin((s.x-q.x)/d);
double ang1 = fix(a+b), ang2 = fix(b-a);
line[i].l = s.x-s.y*tan(ang1);
line[i].r = s.x-s.y*tan(ang2);
}
sort(line,line+n,cmp);
double L = line[0].l, R = line[0].r;
for(int i=0; i<n; i++)
{
if(line[i].l > R)
{
printf("%.2f %.2f\n",L,R);
L = line[i].l, R = line[i].r;
}
else
{
R = max(R,line[i].r);
}
}
printf("%.2f %.2f\n\n",L,R);
}
return 0;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号