510E Fox And Dinner(最大流)

E. Fox And Dinner

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Fox Ciel is participating in a party in Prime Kingdom. There are n foxes there (include Fox Ciel). The i-th fox is a_i years old.

They will have dinner around some round tables. You want to distribute foxes such that:

1. Each fox is sitting at some table.
2. Each table has at least 3 foxes sitting around it.
3. The sum of ages of any two adjacent foxes around each table should be a prime number.

If k foxes f₁, f₂, ..., f_k are sitting around table in clockwise order, then for 1 ≤ i ≤ k - 1: f_i and f_i + 1 are adjacent, and f₁ and f_k are also adjacent.

If it is possible to distribute the foxes in the desired manner, find out a way to do that.

Input

The first line contains single integer n (3 ≤ n ≤ 200): the number of foxes in this party.

The second line contains n integers a_i (2 ≤ a_i ≤ 10⁴).

Output

If it is impossible to do this, output "Impossible".

Otherwise, in the first line output an integer m (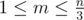): the number of tables.

Then output m lines, each line should start with an integer k -=– the number of foxes around that table, and then k numbers — indices of fox sitting around that table in clockwise order.

If there are several possible arrangements, output any of them.

Sample test(s)

input

4
3 4 8 9

output

1
4 1 2 4 3

input

5
2 2 2 2 2

output

Impossible

input

12
2 3 4 5 6 7 8 9 10 11 12 13

output

1
12 1 2 3 6 5 12 9 8 7 10 11 4

input

24
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

output

3
6 1 2 3 6 5 4
10 7 8 9 12 15 14 13 16 11 10
8 17 18 23 22 19 20 21 24

Note

In example 1, they can sit around one table, their ages are: 3-8-9-4, adjacent sums are: 11, 17, 13 and 7, all those integers are primes.

In example 2, it is not possible: the sum of 2+2 = 4 is not a prime number.

题意：给你n个数字,你能否将它们分为若干个圈,每个圈至少3个数字,每个数字与它相邻的数字和为素数,问你能否有解,输出任意一种。

思路：虽然n不大,但没什么思路,看到提示的算法是网络流,实在还是难以理解,研究了很久才明白这里是利用了----能组合成素数一定是一奇一偶,每个数都与两个数相邻,的性质,将源点与奇数相连,流量为2,汇点与偶数相连,流量也为2,将和为素数的奇数和偶数相连,流量为1,这里的边都是单向的！最后跑最大流看能否有解,根据你最大流的有1流量的边来分集合。

代码：

 

#include<iostream>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<cstring>
using namespace std;

const int MAXN = 230;//点数的最大值
const int MAXM = 42000;//边数的最大值
const int INF = 0x3f3f3f3f;
struct Edge
{
    int to,next,cap,flow;
} edge[MAXM]; //注意是MAXM
int tol;
int head[MAXN];
int gap[MAXN],dep[MAXN],pre[MAXN],cur[MAXN];
void init()
{
    tol = 0;
    memset(head,-1,sizeof(head));
}
//加边，单向图三个参数，双向图四个参数
void addedge(int u,int v,int w,int rw=0)
{
    edge[tol].to = v;
    edge[tol].cap = w;
    edge[tol].next = head[u];
    edge[tol].flow = 0;
    head[u] = tol++;
    edge[tol].to = u;
    edge[tol].cap = rw;
    edge[tol].next = head[v];
    edge[tol].flow = 0;
    head[v]=tol++;
}
//输入参数：起点、终点、点的总数
//点的编号没有影响，只要输入点的总数
int sap(int start,int end,int N)
{
    memset(gap,0,sizeof(gap));
    memset(dep,0,sizeof(dep));
    memcpy(cur,head,sizeof(head));
    int u = start;
    pre[u] = -1;
    gap[0] = N;
    int ans = 0;
    while(dep[start] < N)
    {
        if(u == end)
        {
            int Min = INF;
            for(int i = pre[u]; i != -1; i = pre[edge[i^1].to])
                if(Min > edge[i].cap - edge[i].flow)
                    Min = edge[i].cap - edge[i].flow;
            for(int i = pre[u]; i != -1; i = pre[edge[i^1].to])
            {
                edge[i].flow += Min;
                edge[i^1].flow -= Min;
            }
            u = start;
            ans += Min;
            continue;
        }
        bool flag = false;
        int v;
        for(int i = cur[u]; i != -1; i = edge[i].next)
        {
            v = edge[i].to;
            if(edge[i].cap - edge[i].flow && dep[v]+1 == dep[u])
            {
                flag = true;
                cur[u] = pre[v] = i;
                break;
            }
        }
        if(flag)
        {
            u = v;
            continue;
        }
        int Min = N;
        for(int i = head[u]; i != -1; i = edge[i].next)
            if(edge[i].cap - edge[i].flow && dep[edge[i].to] < Min)
            {
                Min = dep[edge[i].to];
                cur[u] = i;
            }
        gap[dep[u]]--;
        if(!gap[dep[u]])return ans;
        dep[u] = Min+1;
        gap[dep[u]]++;
        if(u != start) u = edge[pre[u]^1].to;
    }

    return ans;
}
bool isPrime(int x)
{
    for (int i = 2; i * i <= x; i++)
        if (x % i == 0)
            return false;
    return true;
}
int a[MAXM],vis[MAXN];
int start,end;
vector<vector<int> > out;

void getOut(int n)
{
    vis[n] = 1;
    int last = (int) out.size() - 1;
    out[last].push_back(n + 1);
    for (int i = head[n]; i != -1; i = edge[i].next)
    {
        int t = edge[i].to;
        if (vis[t] || t == start || t == end)
            continue;
        if(abs(edge[i].flow)==1)
            getOut(t);
    }
}
void check()
{
    for(int i=0; i<tol; i++)
    {
        if(abs(edge[i].flow)==1)
        printf("i=%d , to=%d , flow=%d\n",i,edge[i].to+1,edge[i].flow);
    }
}
int main()
{
#ifndef ONLINE_JUDGE
     freopen("in.txt", "r", stdin);
#endif
    init();
    int n;
    cin >> n;
    start = n + 1;//别用MAXN+1 ! 会超过数组范围出错
    end = n + 2;
    for(int i=0; i<n; i++)
    {
        cin >> a[i];
        if(a[i] % 2)
            addedge(start,i,2);
        else
            addedge(i,end,2);
    }
    for (int i = 0; i < n; i++)
    {
        if (a[i] % 2 == 0)
            continue;
        for (int j = 0; j < n; j++)
            if (isPrime(a[i] + a[j]))
                addedge(i, j, 1);
    }
    int ans = sap(start,end,n+2);
    if(ans < n)
    {
        cout << "Impossible" << endl;
        return 0;
    }
    //check();
    for (int i = 0; i < n; i++)
        if (vis[i] == 0)
            out.push_back(vector<int>()), getOut(i);
    cout << out.size() << endl;
    for (int i = 0; i < (int) out.size(); i++)
    {
        cout << out[i].size();
        for (int j = 0; j < (int) out[i].size(); j++)
            cout << " " << out[i][j];
        cout << endl;
    }
    return 0;
}