HDU 4196 Remoteland (素数筛选+快速幂+费马小定理)
Remoteland
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 262144/131072 K (Java/Others)
Total Submission(s): 1112 Accepted Submission(s): 419
Problem Description
In the Republic of Remoteland, the people celebrate their independence day every year. However, as it was a long long time ago, nobody can remember when it was exactly. The only thing people can remember is that today, the number of days elapsed since their independence (D) is a perfect square, and moreover it is the largest possible such number one can form as a product of distinct numbers less than or equal to n.
As the years in Remoteland have 1,000,000,007 days, their citizens just need D modulo 1,000,000,007. Note that they are interested in the largest D, not in the largest D modulo 1,000,000,007.
As the years in Remoteland have 1,000,000,007 days, their citizens just need D modulo 1,000,000,007. Note that they are interested in the largest D, not in the largest D modulo 1,000,000,007.
Input
Every test case is described by a single line with an integer n, (1<=n<=10,000, 000). The input ends with a line containing 0.
Output
For each test case, output the number of days ago the Republic became independent, modulo 1,000,000,007, one per line.
Sample Input
4 9348095 6297540 0
Sample Output
4 177582252 644064736题意:从1-n里面选数,数的乘积要求是完全平方,求这个乘积的最大值,要求mod 1000000007。也就是 N! 中质数个数为偶数保留,为奇数的去掉一个,最后结果就是 N! /(要除去的数的乘积) ,由于数很大都超过了long long的范围,取模之后做的除法结果不对,这里就用到了费马小定理。先了解一下知识:(by 百科)费马小定理(Fermat Theory)是数论中的一个重要定理,其内容为: 假如p是质数,且Gcd(a,p)=1,那么 a(p-1) ≡1(mod p)。即:假如a是整数,p是质数,且a,p互质(即两者只有一个公约数1),那么a的(p-1)次方除以p的余数恒等于1。费马小定理是数论中的一个定理:假如a是一个整数,p是一个质数,那么
是p的倍数,可以表示为
如果a不是p的倍数,这个定理也可以写成
这题推理过程:
考虑 c%mod=(a%mod)*(b%mod); 令A=a%mod; B=b%mod;C=c%mod;
则 A=a%mod=(a*1)%mod=a%mod*1%mod=(a%mod)*(b^(mod-1))%mod --------因为(b^(mod-1))%mod=1,费马小定理。
=(a*b)%mod*(b^(mod-2))%mod=(c%mod)*(b%mod)^(mod-2)%mod = C*B^(mod-2)
代码:
View Code#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <math.h>
using namespace std;
#define LL long long
const int mod = 1000000007;
const int N = 10000005;
LL fac[N];
int prime[N+1];
void getPrime()//素数筛选,存在小于等于MAXN的素数,prime[0] 存的是素数的个数
{
memset(prime,0,sizeof(prime));
for(int i=2; i<=N; i++)
{
if(!prime[i])prime[++prime[0]]=i;
for(int j=1; j<=prime[0]&&prime[j]<=N/i; j++)
{
prime[prime[j]*i]=1;
if(i%prime[j]==0) break;
}
}
}
int getsum(int n,int p)//这里巧妙的求了 1~n 内的各个数能用 p的 k 次方表示的 k 的数目和
{
int sum = 0;
while(n)
{
sum += n / p;
n /= p;
}
return sum;
}
LL Powmod(LL a,LL b)
{
LL ans = 1;
while(b)
{
if(b & 1)
ans = (ans * a) % mod;
a = (a * a) % mod;
b >>= 1;
}
return ans;
}
int main()
{
//freopen("in.txt","r",stdin);
fac[0] = 1;
for(int i=1; i<N; i++)
{
fac[i] = fac[i-1] * i % mod;
}
int n;
getPrime();
while(~scanf("%d",&n) && n)
{
LL ret = 1;
for(int i=1; i <= prime[0] && prime[i] <= n; i++)
{
int cnt = getsum(n,prime[i]);
if(cnt & 1)
ret = (ret * prime[i]) % mod;
}
printf("%I64d\n",fac[n] * Powmod(ret ,mod - 2) % mod);
}
return 0;
}



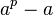 是p的倍数,可以表示为
是p的倍数,可以表示为




 浙公网安备 33010602011771号
浙公网安备 33010602011771号