POJ 3384 Feng Shui(多边形放下2个圆+半平面交)

Feng Shui

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 4532		Accepted: 1390		Special Judge

Description

Feng shui is the ancient Chinese practice of placement and arrangement of space to achieve harmony with the environment. George has recently got interested in it, and now wants to apply it to his home and bring harmony to it.

There is a practice which says that bare floor is bad for living area since spiritual energy drains through it, so George purchased two similar round-shaped carpets (feng shui says that straight lines and sharp corners must be avoided). Unfortunately, he is unable to cover the floor entirely since the room has shape of a convex polygon. But he still wants to minimize the uncovered area by selecting the best placing for his carpets, and asks you to help.

You need to place two carpets in the room so that the total area covered by both carpets is maximal possible. The carpets may overlap, but they may not be cut or folded (including cutting or folding along the floor border) — feng shui tells to avoid straight lines.

Input

The first line of the input file contains two integer numbers n and r — the number of corners in George’s room (3 ≤ n ≤ 100) and the radius of the carpets (1 ≤ r ≤ 1000, both carpets have the same radius). The following n lines contain two integers x_i and y_i each — coordinates of the i-th corner (−1000 ≤ x_i, y_i ≤ 1000). Coordinates of all corners are different, and adjacent walls of the room are not collinear. The corners are listed in clockwise order.

Output

Write four numbers x₁, y₁, x₂, y₂ to the output file, where (x₁, y₁) and (x₂, y₂) denote the spots where carpet centers should be placed. Coordinates must be precise up to 4 digits after the decimal point.

If there are multiple optimal placements available, return any of them. The input data guarantees that at least one solution exists.

Sample Input

#1
5 2
-2 0
-5 3
0 8
7 3
5 0
#2
4 3
0 0
0 8
10 8
10 0

Sample Output

#1
-2 3 3 2.5
#2
3 5 7 3

Hint

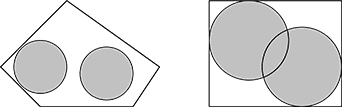
Source

Northeastern Europe 2006, Northern Subregion

 

题意：给出一个凸多边形的房间，根据风水要求，把两个圆形地毯铺在房间里，不能折叠，不能切割，可以重叠。问最多能覆盖多大空间，输出两个地毯的圆心坐标。多组解输出其中一个。

 

思路： 跟上道题一样,先做r的内移线切割,剩下的多边形核找出最远的两点即为两个圆心。这题目输出的坐标好怪。。看不懂。。。

 

代码：

#include<stdio.h>
#include<math.h>
#include<map>
#include<iostream>
#include<string.h>
using namespace std;
const int N = 1505;
const double eps = 1e-8;
const double PI = acos(-1.0);
int sgn(double x)
{
    if(fabs(x) < eps)return 0;
    if(x < 0)return -1;
    else return 1;
}
struct Point
{
    double x,y;
    Point() {}
    Point(double _x,double _y)
    {
        x = _x;
        y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x,y - b.y);
    }
    double operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
};
//计算多边形面积
double CalcArea(Point p[],int n)
{
    double res = 0;
    for(int i = 0; i < n; i++)
        res += (p[i]^p[(i+1)%n]);
    return fabs(res/2);
}
//通过两点，确定直线方程
void Get_equation(Point p1,Point p2,double &a,double &b,double &c)
{
    a = p2.y - p1.y;
    b = p1.x - p2.x;
    c = p2.x*p1.y - p1.x*p2.y;
}
//求交点
Point Intersection(Point p1,Point p2,double a,double b,double c)
{
    double u = fabs(a*p1.x + b*p1.y + c);
    double v = fabs(a*p2.x + b*p2.y + c);
    Point t;
    t.x = (p1.x*v + p2.x*u)/(u+v);
    t.y = (p1.y*v + p2.y*u)/(u+v);
    return t;
}
Point tp[N],p[N],q[N];
void Cut(double a,double b,double c,Point p[],int &cnt)
{
    int tmp = 0;
    for(int i = 1; i <= cnt; i++)
    {
//当前点在左侧，逆时针的点
        if(a*p[i].x + b*p[i].y + c < eps)tp[++tmp] = p[i];
        else
        {
            if(a*p[i-1].x + b*p[i-1].y + c < -eps)//如果p[i-1]在直线的左侧的话，
                //则将p[i],p[i-1]形成的直线与已知直线的交点作为核的一个顶点(这样的话，由于精度的问题，核的面积可能会有所减少)
                tp[++tmp] = Intersection(p[i-1],p[i],a,b,c);
            if(a*p[i+1].x + b*p[i+1].y + c < -eps)
                tp[++tmp] = Intersection(p[i],p[i+1],a,b,c);
        }
    }
    for(int i = 1; i <= tmp; i++)
        p[i] = tp[i];
    p[0] = p[tmp];
    p[tmp+1] = p[1];
    cnt = tmp;
}
double dist(Point a,Point b)
{
    return sqrt((a-b)*(a-b));
}
void Change_dir(Point p[],int n)
{
    for(int i=1; i<=n/2; i++)
        swap(p[i],p[n+1-i]);
}
void solve(Point p[],int n,double r)
{
    Change_dir(p,n);
    p[n+1]=p[1];
    p[0]=p[n];//这里p[0]=p[n]不能少..不然cut会出错
    int cnt=n;
    for(int i=0; i<=n+1; i++) q[i]=p[i];
    for(int i=1; i<=n; i++)
    {
        double a,b,c;
        Point q1,q2;
        double xx = p[i+1].x-p[i].x;
        double yy = p[i+1].y-p[i].y;
        double dd = sqrt(xx*xx+yy*yy);
        q1.x = p[i].x + r*(-yy)/dd, q1.y = p[i].y + r*(xx)/dd;
        q2.x = p[i+1].x + r*(-yy)/dd, q2.y = p[i+1].y + r*(xx)/dd;
        // printf("q1.x=%lf,q1.y=%lf,q2.x=%lf,q2.y=%lf\n",q1.x,q1.y,q2.x,q2.y);
        Get_equation(q1,q2,a,b,c);
        Cut(a,b,c,q,cnt);
        // printf("r=%lf, i=%d,a=%lf,b=%lf,c=%lf,  cnt=%d\n",r,i,a,b,c,cnt);
    }
    double ans=0;
    Point s1,s2;
    for(int i=1; i<=cnt; i++)
        for(int j=1; j<=cnt; j++)
            if(dist(q[i],q[j])>ans)
            {
                ans = dist(q[i],q[j]);
                s1=q[i],s2=q[j];
            }
    printf("%.4lf %.4lf %.4lf %.4lf\n",s1.x,s1.y,s2.x,s2.y);//提交G++记得改为%f
}
int main()
{
    freopen("in.txt","r",stdin);
    int n,r;
    while(scanf("%d%d",&n,&r)!=EOF)
    {
        for(int i=1; i<=n; i++)
            scanf("%lf%lf",&p[i].x,&p[i].y);
        solve(p,n,r);
    }
    return 0;
}