HDU 4667 Building Fence (凸包周长,圆和三角形)
Building Fence
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 1848 Accepted Submission(s): 383
Special Judge
Problem Description
Long long ago, there is a famous farmer named John. He owns a big farm and many cows. There are two kinds of cows on his farm, one is Friesian, and another one is Ayrshire. Each cow has its own territory. In detail, the territory of Friesian is a circle, and of Ayrshire is a triangle. It is obvious that each cow doesn't want their territory violated by others, so the territories won't intersect.
Since the winter is falling, FJ has to build a fence to protect all his cows from hungry wolves, making the territory of cows in the fence. Due to the financial crisis, FJ is currently lack of money, he wants the total length of the fence minimized. So he comes to you, the greatest programmer ever for help. Please note that the part of fence don't have to be a straight line, it can be a curve if necessary.
Since the winter is falling, FJ has to build a fence to protect all his cows from hungry wolves, making the territory of cows in the fence. Due to the financial crisis, FJ is currently lack of money, he wants the total length of the fence minimized. So he comes to you, the greatest programmer ever for help. Please note that the part of fence don't have to be a straight line, it can be a curve if necessary.
Input
The input contains several test cases, terminated by EOF. The number of test cases does not exceed 20.
Each test case begins with two integers N and M(0 ≤ N, M ≤ 50, N + M > 0)which denotes the number of the Friesian and Ayrshire respectively. Then follows N + M lines, each line representing the territory of the cow. Each of the first N lines contains three integers Xi, Yi, Ri(1 ≤ Ri ≤ 500),denotes the coordinates of the circle's centre and radius. Then each of the remaining M lines contains six integers X1i, Y1i, X2i, Y2i, X3i, Y3i, denotes the coordinates of the triangle vertices. The absolute value of the coordinates won't exceed 10000.
Each test case begins with two integers N and M(0 ≤ N, M ≤ 50, N + M > 0)which denotes the number of the Friesian and Ayrshire respectively. Then follows N + M lines, each line representing the territory of the cow. Each of the first N lines contains three integers Xi, Yi, Ri(1 ≤ Ri ≤ 500),denotes the coordinates of the circle's centre and radius. Then each of the remaining M lines contains six integers X1i, Y1i, X2i, Y2i, X3i, Y3i, denotes the coordinates of the triangle vertices. The absolute value of the coordinates won't exceed 10000.
Output
For each test case, print a single line containing the minimal fence length. Your output should have an absolute error of at most 1e-3.
Sample Input
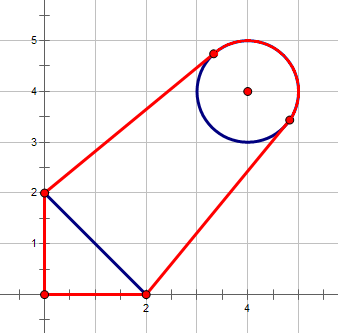
1 1 4 4 1 0 0 0 2 2 0
Sample Output
15.66692HintPlease see the sample picture for more details, the fence is highlighted with red.
Source
题意:给出n个圆和m个三角形,然后用篱笆把它们围起来,问需要最短的篱笆长度是多少。
思路:这题标程应该是求出每个三角形的每个顶点与每个圆的切点和两两圆之间的切点,然后切点来做凸包,最后把凸包上的点的距离加起来,蛮麻烦,其实把圆分成2000个点,
最后一起做凸包也可以水过,前提是你的模版要快,我用的是kuangbin的板子,bin神的凸包板子似乎速率不快(可能是比较准确...),所以就把圆分成500份,当最后凸包点是属于同
一个圆就算弧长,减小误差。
代码:1000点就超1000MS了,只能分成500点 702MS

#include <cmath>
#include <cstdio>
#include <cstring>
#include <string>
#include <queue>
#include <functional>
#include <set>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const double eps = 1e-8;
const double PI = acos(-1.0);
int sgn(double x)
{
if(fabs(x) < eps)return 0;
if(x < 0)return -1;
else return 1;
}
struct Point
{
int id;
double x,y;
Point() {}
Point(double _x,double _y)
{
x = _x;
y = _y;
}
Point operator -(const Point &b)const
{
return Point(x - b.x,y - b.y);
}
double operator ^(const Point &b)const
{
return x*b.y - y*b.x;
}
double operator *(const Point &b)const
{
return x*b.x + y*b.y;
}
};
double dist(Point a,Point b)
{
return sqrt((a-b)*(a-b));
}
const int MAXN = 500010;
Point list[MAXN];
int Stack[MAXN],top;
//相对于list[0]的极角排序
bool _cmp(Point p1,Point p2)
{
double tmp = (p1-list[0])^(p2-list[0]);
if(sgn(tmp) > 0)return true;
else if(sgn(tmp) == 0 && sgn(dist(p1,list[0]) - dist(p2,list[0])) <= 0)
return true;
else return false;
}
void Graham(int n)
{
Point p0;
int k = 0;
p0 = list[0];
for(int i = 1; i < n; i++)
{
if( (p0.y > list[i].y) || (p0.y == list[i].y && p0.x > list[i].x) )
{
p0 = list[i];
k = i;
}
}
swap(list[k],list[0]);
sort(list+1,list+n,_cmp);
if(n == 1)
{
top = 1;
Stack[0] = 0;
return;
}
if(n == 2)
{
top = 2;
Stack[0] = 0;
Stack[1] = 1;
return ;
}
Stack[0] = 0;
Stack[1] = 1;
top = 2;
for(int i = 2; i < n; i++)
{
while(top > 1 && sgn((list[Stack[top-1]]-list[Stack[top-2]])^(list[i]-list[Stack[top-2]])) <= 0)
top--;
Stack[top++] = i;
}
}
double pi = 2*PI/500;
double r[100];
int main()
{
//freopen("in.txt","r",stdin);
int n,m,cnt;
double x,y,x0,x1,x2,y0,y1,y2;
while(~scanf("%d%d",&n,&m))
{
cnt=0;
for(int i=0; i<n; i++)
{
scanf("%lf%lf%lf",&x,&y,&r[i]);
for(double j=0; j<2*PI; j+=pi)
{
list[cnt].id = i;
list[cnt].x = x + r[i]*cos(j);
list[cnt++].y = y + r[i]*sin(j);
}
}
for(int i=0; i<m; i++)
{
scanf("%lf%lf%lf%lf%lf%lf",&x0,&y0,&x1,&y1,&x2,&y2);
list[cnt].id = -1,list[cnt].x=x0,list[cnt++].y=y0;
list[cnt].id = -1,list[cnt].x=x1,list[cnt++].y=y1;
list[cnt].id = -1,list[cnt].x=x2,list[cnt++].y=y2;
}
Graham(cnt);
double ans=0;
for(int i=0; i<top; i++)
{
if(list[Stack[i]].id!= -1 && list[Stack[i]].id == list[Stack[(i+1)%top]].id)
ans+=pi/(2*PI)*(2*PI*r[list[Stack[i]].id]);
else
ans+=dist(list[Stack[i]],list[Stack[(i+1)%top]]);
}
printf("%.5lf\n",ans);
}
return 0;
}
View Code#include <cstdio>
#include <cstring>
#include <string>
#include <queue>
#include <functional>
#include <set>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const double eps = 1e-8;
const double PI = acos(-1.0);
int sgn(double x)
{
if(fabs(x) < eps)return 0;
if(x < 0)return -1;
else return 1;
}
struct Point
{
int id;
double x,y;
Point() {}
Point(double _x,double _y)
{
x = _x;
y = _y;
}
Point operator -(const Point &b)const
{
return Point(x - b.x,y - b.y);
}
double operator ^(const Point &b)const
{
return x*b.y - y*b.x;
}
double operator *(const Point &b)const
{
return x*b.x + y*b.y;
}
};
double dist(Point a,Point b)
{
return sqrt((a-b)*(a-b));
}
const int MAXN = 500010;
Point list[MAXN];
int Stack[MAXN],top;
//相对于list[0]的极角排序
bool _cmp(Point p1,Point p2)
{
double tmp = (p1-list[0])^(p2-list[0]);
if(sgn(tmp) > 0)return true;
else if(sgn(tmp) == 0 && sgn(dist(p1,list[0]) - dist(p2,list[0])) <= 0)
return true;
else return false;
}
void Graham(int n)
{
Point p0;
int k = 0;
p0 = list[0];
for(int i = 1; i < n; i++)
{
if( (p0.y > list[i].y) || (p0.y == list[i].y && p0.x > list[i].x) )
{
p0 = list[i];
k = i;
}
}
swap(list[k],list[0]);
sort(list+1,list+n,_cmp);
if(n == 1)
{
top = 1;
Stack[0] = 0;
return;
}
if(n == 2)
{
top = 2;
Stack[0] = 0;
Stack[1] = 1;
return ;
}
Stack[0] = 0;
Stack[1] = 1;
top = 2;
for(int i = 2; i < n; i++)
{
while(top > 1 && sgn((list[Stack[top-1]]-list[Stack[top-2]])^(list[i]-list[Stack[top-2]])) <= 0)
top--;
Stack[top++] = i;
}
}
double pi = 2*PI/500;
double r[100];
int main()
{
//freopen("in.txt","r",stdin);
int n,m,cnt;
double x,y,x0,x1,x2,y0,y1,y2;
while(~scanf("%d%d",&n,&m))
{
cnt=0;
for(int i=0; i<n; i++)
{
scanf("%lf%lf%lf",&x,&y,&r[i]);
for(double j=0; j<2*PI; j+=pi)
{
list[cnt].id = i;
list[cnt].x = x + r[i]*cos(j);
list[cnt++].y = y + r[i]*sin(j);
}
}
for(int i=0; i<m; i++)
{
scanf("%lf%lf%lf%lf%lf%lf",&x0,&y0,&x1,&y1,&x2,&y2);
list[cnt].id = -1,list[cnt].x=x0,list[cnt++].y=y0;
list[cnt].id = -1,list[cnt].x=x1,list[cnt++].y=y1;
list[cnt].id = -1,list[cnt].x=x2,list[cnt++].y=y2;
}
Graham(cnt);
double ans=0;
for(int i=0; i<top; i++)
{
if(list[Stack[i]].id!= -1 && list[Stack[i]].id == list[Stack[(i+1)%top]].id)
ans+=pi/(2*PI)*(2*PI*r[list[Stack[i]].id]);
else
ans+=dist(list[Stack[i]],list[Stack[(i+1)%top]]);
}
printf("%.5lf\n",ans);
}
return 0;
}
这个是别人的代码,2000点暴力水过的,板子蛮快 655MS

#include<iostream>
#include<algorithm>
#include<string.h>
#include<stack>
#include<queue>
#include<math.h>
#include<cstdio>
#define maxn 500000
using namespace std;
const double PI=acos(-1.0);
const double eps=1e-7;
struct point
{
double x, y;
}p[maxn],res[maxn];
double dist(point a,point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
bool mult(point sp, point ep, point op)
{
return (sp.x - op.x) * (ep.y - op.y)
>= (ep.x - op.x) * (sp.y - op.y);
}
bool operator < (const point &l, const point &r)
{
return l.y < r.y || (l.y == r.y && l.x < r.x);
}
int graham(point pnt[], int n, point res[])
{
int i, len, k = 0, top = 1;
sort(pnt, pnt + n);
if (n == 0) return 0; res[0] = pnt[0];
if (n == 1) return 1; res[1] = pnt[1];
if (n == 2) return 2; res[2] = pnt[2];
for (i = 2; i < n; i++)
{
while (top && mult(pnt[i], res[top], res[top-1]))
top--;
res[++top] = pnt[i];
}
len = top; res[++top] = pnt[n - 2];
for (i = n - 3; i >= 0; i--)
{
while (top!=len && mult(pnt[i], res[top],res[top-1]))
top--;
res[++top] = pnt[i];
}
return top;
}
double pi = 2*PI/2000;
int main()
{
//freopen("in.txt","r",stdin);
int n,m,e;
double x,y,r,x0,y0,x1,x2,y1,y2;
while(~scanf("%d%d",&n,&m))
{
e=0;
for(int i=0;i<n;i++)
{
scanf("%lf%lf%lf",&x,&y,&r);
for(double j=0;j<2*PI;j+=pi)
{
p[e].x=x+r*cos(j);
p[e++].y=y+r*sin(j);
}
}
for(int i=1;i<=m;i++)
{
scanf("%lf%lf%lf%lf%lf%lf",&x0,&y0,&x1,&y1,&x2,&y2);
p[e].x=x0;
p[e++].y=y0;
p[e].x=x1;
p[e++].y=y1;
p[e].x=x2;
p[e++].y=y2;
}
int cnt=graham(p,e,res);
double ans=0;
for(int i=0;i<cnt;i++)
ans+=dist(res[i],res[i+1]);
ans+=dist(res[0],res[cnt]);
printf("%.5lf\n",ans);
}
return 0;
}
#include<algorithm>
#include<string.h>
#include<stack>
#include<queue>
#include<math.h>
#include<cstdio>
#define maxn 500000
using namespace std;
const double PI=acos(-1.0);
const double eps=1e-7;
struct point
{
double x, y;
}p[maxn],res[maxn];
double dist(point a,point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
bool mult(point sp, point ep, point op)
{
return (sp.x - op.x) * (ep.y - op.y)
>= (ep.x - op.x) * (sp.y - op.y);
}
bool operator < (const point &l, const point &r)
{
return l.y < r.y || (l.y == r.y && l.x < r.x);
}
int graham(point pnt[], int n, point res[])
{
int i, len, k = 0, top = 1;
sort(pnt, pnt + n);
if (n == 0) return 0; res[0] = pnt[0];
if (n == 1) return 1; res[1] = pnt[1];
if (n == 2) return 2; res[2] = pnt[2];
for (i = 2; i < n; i++)
{
while (top && mult(pnt[i], res[top], res[top-1]))
top--;
res[++top] = pnt[i];
}
len = top; res[++top] = pnt[n - 2];
for (i = n - 3; i >= 0; i--)
{
while (top!=len && mult(pnt[i], res[top],res[top-1]))
top--;
res[++top] = pnt[i];
}
return top;
}
double pi = 2*PI/2000;
int main()
{
//freopen("in.txt","r",stdin);
int n,m,e;
double x,y,r,x0,y0,x1,x2,y1,y2;
while(~scanf("%d%d",&n,&m))
{
e=0;
for(int i=0;i<n;i++)
{
scanf("%lf%lf%lf",&x,&y,&r);
for(double j=0;j<2*PI;j+=pi)
{
p[e].x=x+r*cos(j);
p[e++].y=y+r*sin(j);
}
}
for(int i=1;i<=m;i++)
{
scanf("%lf%lf%lf%lf%lf%lf",&x0,&y0,&x1,&y1,&x2,&y2);
p[e].x=x0;
p[e++].y=y0;
p[e].x=x1;
p[e++].y=y1;
p[e].x=x2;
p[e++].y=y2;
}
int cnt=graham(p,e,res);
double ans=0;
for(int i=0;i<cnt;i++)
ans+=dist(res[i],res[i+1]);
ans+=dist(res[0],res[cnt]);
printf("%.5lf\n",ans);
}
return 0;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号