500E New Year Domino(单调栈(单调队列)+并查集)

E. New Year Domino

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Celebrating the new year, many people post videos of falling dominoes; Here's a list of them:https://www.youtube.com/results?search_query=New+Years+Dominos

User ainta, who lives in a 2D world, is going to post a video as well.

There are n dominoes on a 2D Cartesian plane. i-th domino (1 ≤ i ≤ n) can be represented as a line segment which is parallel to the y-axis and whose length is l_i. The lower point of the domino is on the x-axis. Let's denote the x-coordinate of the i-th domino as p_i. Dominoes are placed one after another, so p₁ < p₂ < ... < p_n - 1 < p_n holds.

User ainta wants to take a video of falling dominoes. To make dominoes fall, he can push a single domino to the right. Then, the domino will fall down drawing a circle-shaped orbit until the line segment totally overlaps with the x-axis.

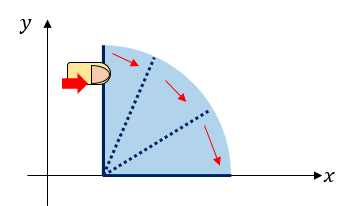
Also, if the s-th domino touches the t-th domino while falling down, the t-th domino will also fall down towards the right, following the same procedure above. Domino s touches domino t if and only if the segment representing s and t intersects.

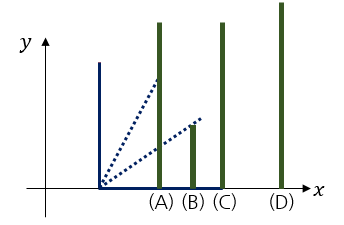
See the picture above. If he pushes the leftmost domino to the right, it falls down, touching dominoes (A), (B) and (C). As a result, dominoes (A), (B), (C) will also fall towards the right. However, domino (D) won't be affected by pushing the leftmost domino, but eventually it will fall because it is touched by domino (C) for the first time.

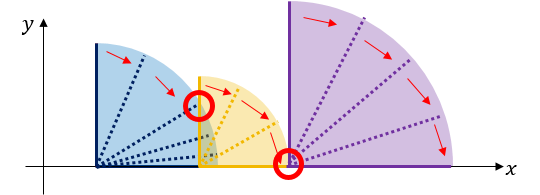
The picture above is an example of falling dominoes. Each red circle denotes a touch of two dominoes.

User ainta has q plans of posting the video. j-th of them starts with pushing the x_j-th domino, and lasts until the y_j-th domino falls. But sometimes, it could be impossible to achieve such plan, so he has to lengthen some dominoes. It costs one dollar to increase the length of a single domino by 1. User ainta wants to know, for each plan, the minimum cost needed to achieve it. Plans are processed independently, i. e. if domino's length is increased in some plan, it doesn't affect its length in other plans. Set of dominos that will fall except x_j-th domino and y_j-th domino doesn't matter, but the initial push should be on domino x_j.

Input

The first line contains an integer n (2 ≤ n ≤ 2 × 10⁵)— the number of dominoes.

Next n lines describe the dominoes. The i-th line (1 ≤ i ≤ n) contains two space-separated integers p_i, l_i (1 ≤ p_i, l_i ≤ 10⁹)— the x-coordinate and the length of the i-th domino. It is guaranteed that p₁ < p₂ < ... < p_n - 1 < p_n.

The next line contains an integer q (1 ≤ q ≤ 2 × 10⁵) — the number of plans.

Next q lines describe the plans. The j-th line (1 ≤ j ≤ q) contains two space-separated integers x_j, y_j (1 ≤ x_j < y_j ≤ n). It means the j-th plan is, to push the x_j-th domino, and shoot a video until the y_j-th domino falls.

Output

For each plan, print a line containing the minimum cost needed to achieve it. If no cost is needed, print 0.

Sample test(s)

input

6
1 5
3 3
4 4
9 2
10 1
12 1
4
1 2
2 4
2 5
2 6

output

0
1
1
2

Note

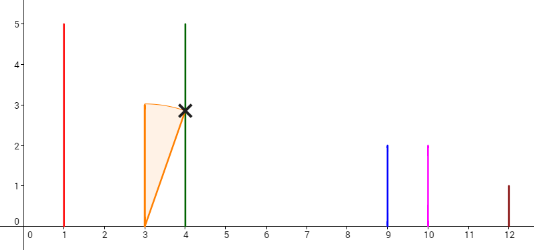
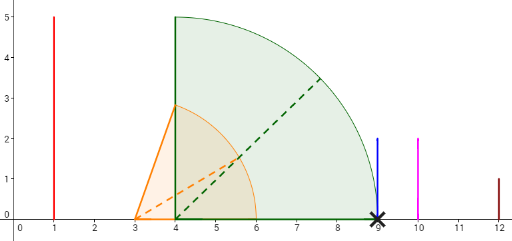
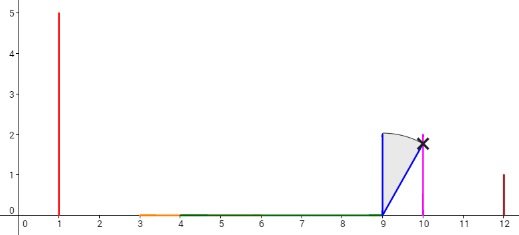
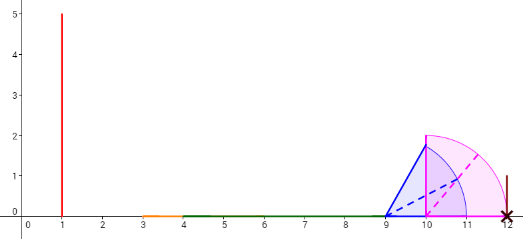
Consider the example. The dominoes are set like the picture below.

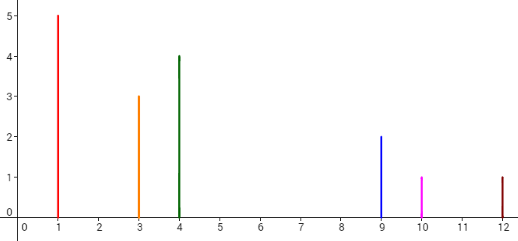
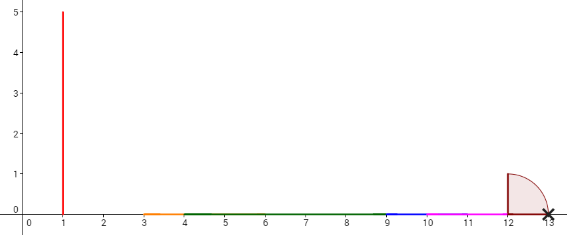
Let's take a look at the 4th plan. To make the 6th domino fall by pushing the 2nd domino, the length of the 3rd domino (whose x-coordinate is 4) should be increased by 1, and the 5th domino (whose x-coordinate is 9) should be increased by 1 (other option is to increase 4th domino instead of 5th also by 1). Then, the dominoes will fall like in the picture below. Each cross denotes a touch between two dominoes. 

题意：给你n张扑克牌,x坐标和扑克牌长度,然后q次询问,刚开始向右翻第x张,最后能否将y张牌翻倒,牌可加长,1单位长花费1,问你最小花费,各询问独立。
 
思路：单调栈(单调队列)+并查集,将会相互翻倒的放在一个集合,记录集合左右端点坐标,利用单调栈从后面往前可实现计算。
 
代码：
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 200005;
struct section
{
    int l,r,id;
} x[N];
vector<int> b[N];
int qx[N],qy[N],se_l[N],se_r[N],fa[N],sum[N],ans[N];
int find(int x)
{
    return x==fa[x]?x:fa[x]=find(fa[x]);
}
int main()
{
    int len,n,m;
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        scanf("%d%d",&x[i].l,&len);
        x[i].r=x[i].l+len;
        fa[i]=i;
    }
    scanf("%d",&m);
    for(int i=1; i<=m; i++)
    {
        scanf("%d%d",&qx[i],&qy[i]);
        b[qx[i]].push_back(i);
    }
    deque<int> que;
    for(int i=n; i>0; i--)
    {
        se_l[i]=x[i].l,se_r[i]=x[i].r;          //se_l[i]表示以i为根的集合左端坐标，se_r[i]为右端
        while(!que.empty() && se_l[que.front()]<=se_r[i]) //新加入的区间最大覆盖后面端点
        {
            se_r[i]=max(se_r[i],se_r[que.front()]);//能碰倒但右端不一定谁长
            fa[find(que.front())]=i;//更新当前集合根
            que.pop_front();
        }
        if(!que.empty())//计算当前集合到最后端点的花费
            sum[i]=sum[que.front()]+se_l[que.front()]-se_r[i];
        else
            sum[i]=0;
        que.push_front(i);//将当前端点加入队列顶端
        for(int j=0; j<b[i].size(); j++)//计算m次询问中开头是 i 的询问
        {
            int id=b[i][j];
            int tmp=qy[id];
            ans[id]=sum[i]-sum[find(tmp)];//区间相减正好是所求结果
            //printf("i=%d,id=%d,tmp=%d,sum[%d]=%d,sum[%d]=%d\n",i,id,tmp,i,sum[i],tmp,sum[find(tmp)]);
        }
    }
    for(int i=1; i<=m; i++)
        printf("%d\n",ans[i]);
}