507D The Maths Lecture (数位DP)
Amr doesn't like Maths as he finds it really boring, so he usually sleeps in Maths lectures. But one day the teacher suspected that Amr is sleeping and asked him a question to make sure he wasn't.
First he gave Amr two positive integers n and k. Then he asked Amr, how many integer numbers x > 0 exist such that:
- Decimal representation of x (without leading zeroes) consists of exactly n digits;
- There exists some integer y > 0 such that:
![]() ;
;- decimal representation of y is a suffix of decimal representation of x.
As the answer to this question may be pretty huge the teacher asked Amr to output only its remainder modulo a number m.
Can you help Amr escape this embarrassing situation?
Input consists of three integers n, k, m (1 ≤ n ≤ 1000, 1 ≤ k ≤ 100, 1 ≤ m ≤ 109).
Print the required number modulo m.
1 2 1000
4
2 2 1000
45
5 3 1103
590
A suffix of a string S is a non-empty string that can be obtained by removing some number (possibly, zero) of first characters from S.
以前自己做过一小段时间的数位DP,但掌握不精。。今天碰到一道,希望弄透,以后写同类题解可能就不详细解释了。
题意:问你n位数,任意尾缀可以被k整除就符合,问给你n,k,m(取模用)你能弄出多少个数字
思路:数据范围,数位DP
代码1(便于理解的DP): dp[i][j][0]代表i位数,被k取余余下j,不存在某个后缀能整除k的个数, dp[i][j][1]代表i位数,被k取余余下j,存在某个后缀能整除k的个数
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <iostream>
using namespace std;
typedef long long ll;
const int N = 1005;
ll dp[N][100][2];
ll n, k, m, ten;
int main()
{
while (~scanf("%d%d%d",&n,&k,&m))
{
ten = 1;
memset(dp, 0, sizeof dp);
dp[0][0][0] = 1;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < k; j++)
{
for (int z = 0; z < 10; z++)//z代表往前面添加的数字
{
if (i == n - 1 && z == 0)continue;
ll now = (z*ten + j) % k;
if (now == 0 && z) //本不符合当添加后符合,前面加1~9都OK
dp[i + 1][now][1] += dp[i][j][0]%m;
else //前面添加0做下一位计算用(算在不符合中),还有添加后还是不符合
dp[i + 1][now][0] += dp[i][j][0]%m;
dp[i + 1][now][1] += dp[i][j][1]%m; //后面尾缀符合了前面就随意添加
}
}
ten = ten * 10LL %k;//ten代表往前添加数字时候要加上z*ten,比如98前加个2就是加上2*100
}
ll ans = 0;
for (int i = 0; i < k; i++)
ans += dp[n][i][1];
printf("%d\n",ans%m);
}
return 0;
}
代码2:这种代码我以前见得比较多,简单巧妙,这里利用了数的范围只会缩小的特点dfs。
#include<stdio.h>
#include<string.h>
int dp[1005][105][2],shi[1005];
int k,MOD,n;
int dfs(int pos,int preMOD,int flag)//pos位数,preMOD前面的余数,flag=1符合,flag=0不符合
{
int tmp,i,ans=0;
if (pos>n) return flag;
if (dp[pos][preMOD][flag]!=-1)
return dp[pos][preMOD][flag];
tmp=(pos==n?1:0); //看是否到最后一位,不然前面不能加0
for (i=tmp; i<=9; i++)
ans=(ans+dfs( pos+1, (preMOD+i*shi[pos-1])%k, flag||((preMOD+i*shi[pos-1])%k==0&&i!=0) ))%MOD;
return dp[pos][preMOD][flag]=ans;
}
int main()
{
int cnt,i;
scanf("%d%d%d",&n,&k,&MOD);
shi[0]=1;
for (i=1; i<=1000; i++) shi[i]=shi[i-1]*10%k;//这里跟代码1的ten作用相同
memset(dp,-1,sizeof(dp));
printf("%d\n",dfs(1,0,0));
}



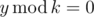 ;
;
 浙公网安备 33010602011771号
浙公网安备 33010602011771号