新生赛补题

cy的上升序列（简单dp）

题目链接：http://acm.nuc.edu.cn/OJ/contest/show/60/1012

题目大意： 构造一个长度为n的严格递增序列，每个数都属于【1,m】。求方案数，结果模998244353。

dp的转移方程：

第一位数 i 代表的是遍历到第几个数了，j代表的是当前位是几。
$$
dp[i][j]=dp[i-1][j]+dp[i][j-1]
$$
AC代码：

#include <iostream>
using namespace std;
const int maxn = 3e3+5;
typedef long long ll;
ll dp[maxn][maxn];
const ll mod = 998244353;

int main(){
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(i==1) dp[i][j]=1;//一个数只有一种情况
			else dp[i][j]=(dp[i-1][j]+dp[i][j-1])%mod; 
		}
	}
	int ans=0;
	for(int i=1;i<=m;i++){
		ans=(ans+dp[n][i])%mod;
	}
	cout<<ans;
	return 0;
}

XiaoMing的和和美美

题目链接：http://acm.nuc.edu.cn/OJ/contest/show/60/1007

题目大意：现在存在 1 - n 这 n 个数，将这n个数分成两组，使得两组得到的两组的加和的数的最大公约数是最大的。

例：n=6， 左边一组：1 6 2 5 =14

​ 右边一组： 3 4 =7 所以最大是7

解题思路：根据多重背包的思想，很容易想出，1到sum（1到n的加和）的所有数都可以在一边表示出来。

题目就转换成了：将一个数分成两个数，使两个数的最大公约数是最大的。 1 - n的数的加和为 n（n+1）/2。

​ n（n+1）/2 的最大公约数肯定是

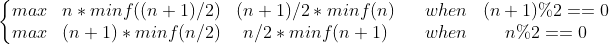
​ minf（n）表示求出n的最大公约数。

注意特判一下n==2的情况。

AC代码：

#include <iostream>
#include <cmath>
using namespace std;
typedef long long ll;

ll minf(ll x){
	for(ll i=2;i<=sqrt(x);i++){
		if(x%i==0){
			return x/i;
		}
	}
	return 1;
}

int main(){
	ll n;
	cin>>n;
	//n *(n+1)/2
	ll ans=0;
	if(n==2){
		cout<<1<<endl;
		return 0;
	}
	if(n%2==0){//让其中的一半乘的数尽可能大（在minf中找到最大公约数）
		ans=max(n/2*minf(n+1),(n+1)*minf(n/2));
	}else{
		ans=max((n+1)/2*minf(n),n*minf((n+1)/2));
	}
	cout<<ans<<endl;
	return 0;
}

简单的异或问题

这题的数据很水，暴力就能过，不过我在dalao那学会了如何快速的求出一个数的二进制形式的时候1的个数。

在这里做个笔记：

快速得到一个数二进制形式的1的个数（每次几乎O（m）复杂度，m是1的个数，差不多 O（1））：

当时憨批的我竟然想的用dp做，把自己搞蒙了

int getone(int x){
	int cnt=0;
	while(x){
		x&=(x-1);
		cnt++;
	}
}

x = 14时 x 1110

​ x - 1 1101 相当于把第一个1后面的数翻转了一次：0 -> 1    1 -> 0,当&操作时变为0

x&(x-1) 1100

lowbit得到第一个1的位置

 int lowbit(int x){
      return x&(-x);
 }

x = 6时 x 110

​ -x 010

x&(-x) 010

题目链接：http://acm.nuc.edu.cn/OJ/contest/show/60/1001

题目大意：存在三种操作，自己看题吧。预处理一下就过了，，迷

AC代码：

#include <iostream>
using namespace std;
const int maxn = 1e5+5;
int s[maxn]; 
int a[maxn];

int get(int x){
	int cnt=0;
	while(x){
		x&=(x-1);
		cnt++;
	}
	return cnt;
}

int main(){
	for(int i=1;i<maxn;i++){
		if(get(i)%2==1){
			s[i]=1;
		}else{
			s[i]=0;
		}
	}
	int n,q;
	scanf("%d%d",&n,&q);
	for(int i=1;i<=n;i++) {
		scanf("%d",&a[i]);
		if(s[i]==0) a[i]=0;	
	}
	int ch,l,r,x,y;
	while(q--){
	scanf("%d",&ch);
		if(ch==1){
			scanf("%d%d",&l,&r);
			int ans=a[l];
			for(int i=l+1;i<=r;i++){
				ans=ans^a[i];
			}
			printf("%d\n",ans);
		}else if(ch==2){
			scanf("%d%d%d",&l,&r,&x);
			for(int i=l;i<=r;i++){
				a[i]=a[i]^x*s[i];
			}
		}else{
			scanf("%d%d",&x,&y);
			if(s[x]==0) a[x]=0;
			else a[x]=y;
		}
	}
	return 0;
}