哈希
提到哈希,相信很多同学都不陌生,hash(散列、杂凑)函数,是将任意长度的数据映射到有限长度的域上。在算法竞赛中被广泛应用。
那hash函数是如何实现将任意长度的数据映射到有限长度的域上的呢?通常是对一个数取模,当然有时会出现冲突,处理冲突的方法一般有两种:一种是拉链法另一种是开放寻址法,下面我将会具体对这两种实现方式作出分析
先来看下拉链法:
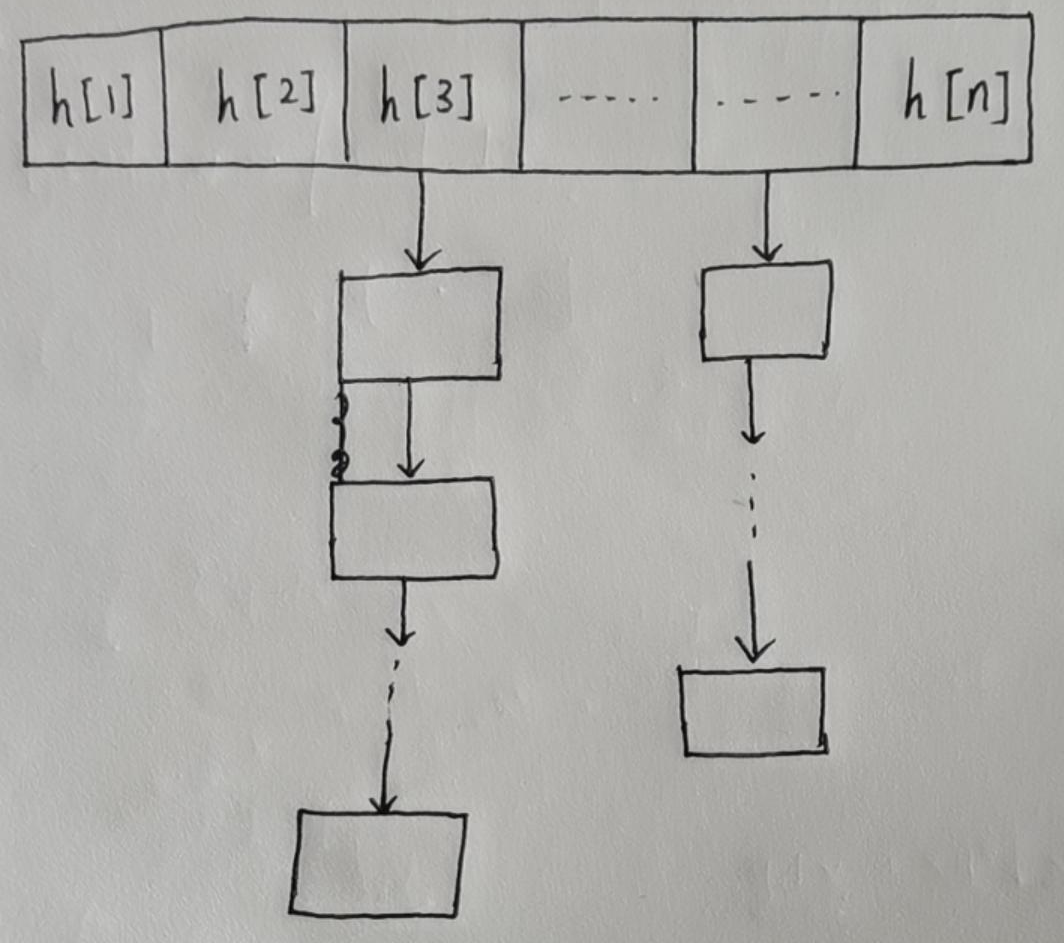
大概就长这个样子,如果m和n经过哈希变换后都变成了k那么他们就会变成h[k]下面链条中的一部分, h[k]储存的就是每一条链表的头节点的位置,具体实现就是用数组模拟链表来实现。
当你需要添加一个元素时,只需将经过哈希变换之后的元素添加至数组中即可,如需查找一个元素,就需要到对应哈希函数映射值下的那条链条中去找。
下面来介绍一下开放寻址法构造哈希表,哈希函数基本上是类似的,但查找与添加元素的方式就有很大的变化了,它不需要在每一个h数组下都加一条链,它只需要找到空位即可,然后按照规则一个一个找就行,如果x在哈希表中find函数返回的就是储存x的数组下标,
如果x不在哈希表中,那么返回的就是x应该存放的位置(也就是按照查找规则发现的第一个空位)
下面给出一道例题并给出两种实现方式:
维护一个集合,支持如下几种操作:
I x,插入一个数 x;Q x,询问数 x 是否在集合中出现过;
现在要进行 NN 次操作,对于每个询问操作输出对应的结果。
输入格式
第一行包含整数 N,表示操作数量。
接下来 N行,每行包含一个操作指令,操作指令为 I x,Q x 中的一种。
输出格式
对于每个询问指令 Q x,输出一个询问结果,如果 xx 在集合中出现过,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤N≤10^5
−10^9≤x≤10^9
输入样例:
5
I 1
I 2
I 3
Q 2
Q 5
输出样例:
Yes
No
拉链法模拟散列表 #include<iostream> #include<cstring> using namespace std; const int N=100003; int h[N],ne[N],e[N],idx; void insert(int x) { //h[k]中存的是k这个结点所生成的链表中第一个元素的下标 int k=(x%N+N)%N; e[idx]=x; ne[idx]=h[k]; h[k]=idx++; } bool query(int x) { int k=(x%N+N)%N; for(int i=h[k];i!=-1;i=ne[i]) if(e[i]==x) return true; return false; } int main() { int n; cin>>n; string c; int d; memset(h,-1,sizeof(h)); for(int i=1;i<=n;i++) { cin>>c>>d; if(c=="I") insert(d); else { if(query(d)) printf("Yes\n"); else printf("No\n"); } } return 0; } //开放寻址法模拟散列表 #include<iostream> #include<cstring> using namespace std; const int N=200003,null=0x3f3f3f3f; int h[N]; //说明:如若x存在,则返回x所在的数组下标,如若不存在,则返回应该插入的位置 int find(int x) { int t=(x%N+N)%N; while(h[t]!=null&&h[t]!=x) { t++; if(t==N) t=0; } return t; } int main() { int n; cin>>n; string c; int d; memset(h,0x3f,sizeof(h)); for(int i=1;i<=n;i++) { cin>>c>>d; int k=find(d); if(c=="I") h[k]=d; else { if(h[k]==d) printf("Yes\n"); else printf("No\n"); } } return 0; }
下面再给出一个与上述两种方式不同的哈希方式:
字符串哈希:
先给出一道例题,代码中有详细讲解:
给定一个长度为 n 的字符串,再给定 m 个询问,每个询问包含四个整数 l1,r1,l2,r2,请你判断 [l1,r1][l1,r1] 和 [l2,r2][l2,r2] 这两个区间所包含的字符串子串是否完全相同。
字符串中只包含大小写英文字母和数字。
输入格式
第一行包含整数 n 和 m,表示字符串长度和询问次数。
第二行包含一个长度为 nn 的字符串,字符串中只包含大小写英文字母和数字。
接下来 m 行,每行包含四个整数 l1,r1,l2,r2,表示一次询问所涉及的两个区间。
注意,字符串的位置从 11 开始编号。
输出格式
对于每个询问输出一个结果,如果两个字符串子串完全相同则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤10^5
输入样例:
8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2
输出样例:
Yes
No
Yes
#include<iostream> #include<cstring> using namespace std; typedef unsigned long long ULL; const int N=100010,P=131; //p通常选择131或者13331;通常选择mod2^64,在ULL中爆掉对结果不产生影响 int n,m; char s[N]; ULL h[N],p[N];//h[i]存储前i个字符的哈希值,p[i]存储p的i次方 ULL fun(int l,int r) { return h[r]-h[l-1]*p[r-l+1]; } int main() { cin>>n>>m>>s+1; p[0]=1; for(int i=1;i<=n;i++) { p[i]=P*p[i-1]; h[i]=h[i-1]*P+s[i]; } int l1,r1,l2,r2; while(m--) { cin>>l1>>r1>>l2>>r2; if(fun(l1,r1)==fun(l2,r2)) printf("Yes\n"); else printf("No\n"); } return 0; }
现在我对这道题的思路以及疑难点进行分析:
我们是将每一个字符转化为p进制下的一个数,然后对2^64进行取余;
注意:p常取131或者13331,在概率论中我们可以看到取这两个质数可以把冲突的概率降低,具体原因我在这就不分析了,这时候就要考验人品了,绝大部分题目用这两个数是没问题的,还需要注意的一点就是,2^64正好是unsigned long long的范围,所以我们可以把数据类型定义为unsigned long long,这样即使他们在运算过程中爆掉也不会对结果产生影响。
我们处理l到r上的哈希值时,采用的是前缀和的形式,字符串左边是高位,右边是低位
下面对哈希函数做出分析:
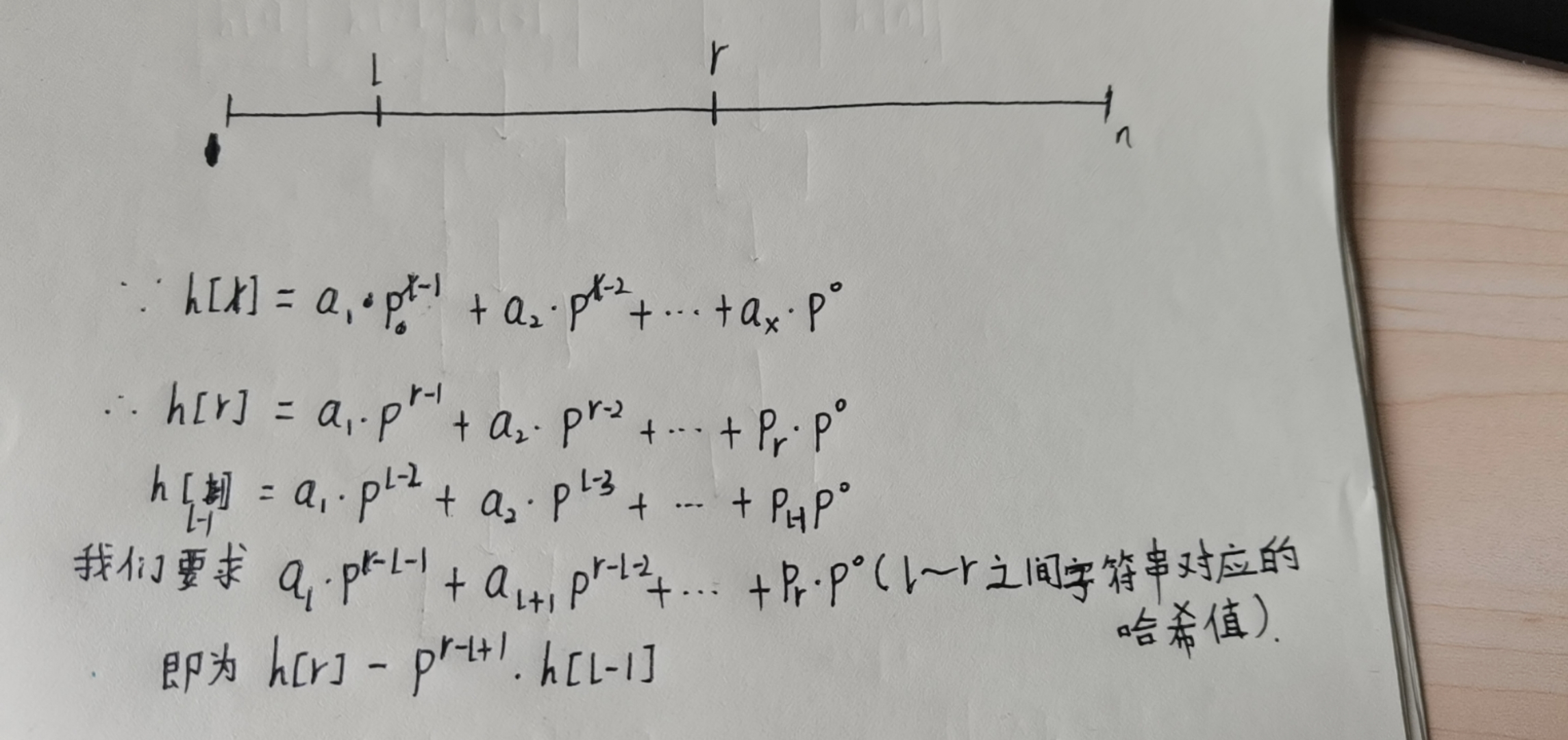
以上就是我对哈希的全部分析啦,希望大家能够喜欢!

