树状数组
今天想跟大家分享的东西是树状数组,什么是树状数组呢?根据名字就能大致推出就是利用我们常见的数组来模拟树状结构。那么他可以解决哪些问题呢?我最后会加以说明。
首先我们来说下树状数组长什么样子呢?
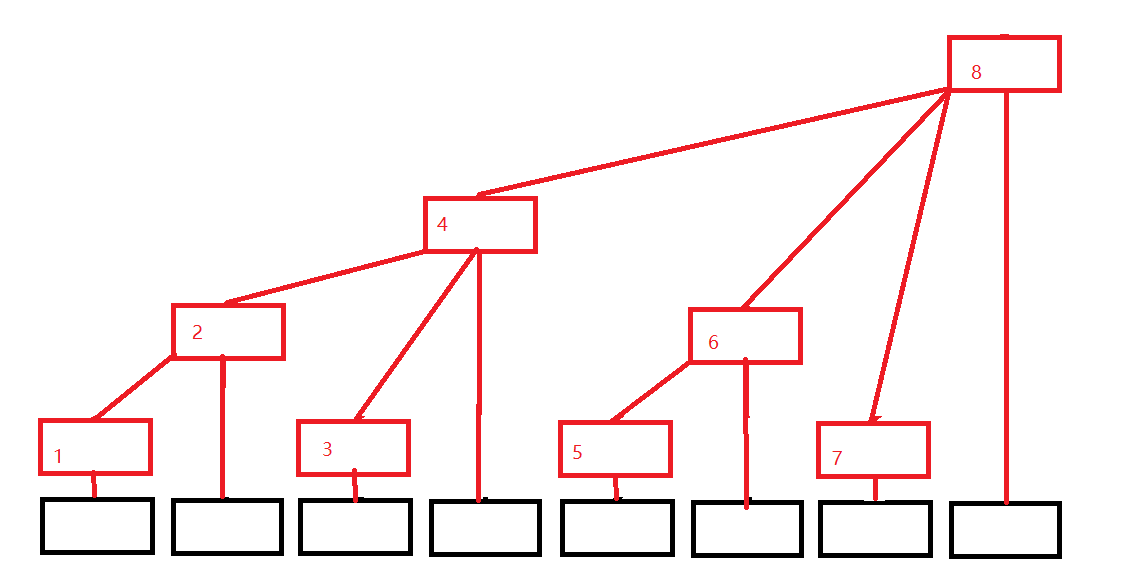
在这副图片上我们可以看到有两种元素的数组,黑颜色的数组代表原来的数组,我们用a[ ]来表示吧,而红颜色的数组代表我们要构造的树状数组,我们用b[ ]来表示。每个红颜色的数组里面存放的是它下面节点元素的和,观察图片不难得出:
c[1]=a[1]
c[2]=c[1]+a[2]=a[1]+a[2]
c[3]=a[3]
c[4]=c[2]+c[3]+a[4]=a[1]+a[2]+a[3]+a[4]
c[5]=a[5]
c[6]=c[5]+a[6]=a[5]+a[6]
c[7]=a[7]
c[8]=c[4]+c[6]+c[7]+a[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
我们现在从上面的一些例子中找一下规律;我们不难发现如果n为2的幂次,那么c[n]=a[1]+a[2]+.....+a[n],那么这样的n在二进制表示下又有什么规律呢?我们发现它的二进制表示中只有最高位是1,其余位均是0,那么这与二进制表示下的数的最低位到最高位有没有什么关系呢?事实上c[n]=a[n-2^m+1]+a[n-2^m+2]+.....+a[n]其中m为n的二进制表示中从低位开始直到找到第一个1为止,这中间的0的长度。
那么这个m该如何求呢,m=n&(-n);举个例子来说:
n为12,则二进制表示为1100,那么它的反码为各位取反,即0011,则此时为1的地方在n中都为0,那么将其反码加1则会使原来n中第一个1及其之前的数保持不变,而之后的数均被取反,那么他们做&运算会保留下第一个为1的数,这也就是lowbit函数的原理啦。
我们常见的区间问题主要有以下几种:
(1)单点更新,单点查询;
(2)单点更新,区间查询 ;
(3)区间更新,单点查询;
(4)区间更新,区间查询;
第一个问题用 一个普通的一维数组即可实现,在这里就不多说了,我主要想介绍一下后三个问题的处理方法。
我们先处理第二个问题,如果我们对a[i]进行修改,我们所构造的数组是储存a数组的和,所以肯定会受到影响,但是哪些元素受到影响了呢?实际上是c[i+2^m],c[i+2^m+2^m]......;不难发现,这个操作恰好可以用lowbit函数解决。下面给出建立树状数组的板子:
int lowbit(int x)//求出x中第一个为1的位置 { return x&(-x); } void update(int x,int k)//构造树状数组 { while(x<=n) { c[x]+=k; x+=lowbit(x); } } int sum(int i)//实现查询 { int res=0; while(i>0) { res+=c[i]; i-=lowbit(i); } return res; }
这就是单点更新,区间查询的板子了。下面给一个例题:(纯模板)洛谷3374
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 xx
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 n,mn,m,分别表示该数列数字的个数和操作的总个数。
第二行包含 nn 个用空格分隔的整数,其中第 ii 个数字表示数列第 ii 项的初始值。
接下来 mm 行每行包含 33 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 xx 个数加上 kk -
2 x y含义:输出区间 [x,y][x,y] 内每个数的和
输入输出样例
5 5 1 5 4 2 3 1 1 3 2 2 5 1 3 -1 1 4 2 2 1 4
14 16
#include<iostream> using namespace std; int a[500010],c[500010]; int n,m; int lowbit(int x) { return x&(-x); } void update(int x,int k) { while(x<=n) { c[x]+=k; x+=lowbit(x); } } int sum(int i) { int res=0; while(i>0) { res+=c[i]; i-=lowbit(i); } return res; } int main() { cin>>n>>m; for(int i=1;i<=n;i++) { cin>>a[i]; update(i,a[i]);//每输入一次值就更新一次所构造的数组 } int a,b,c; while(m--) { cin>>a>>b>>c; if(a==1) update(b,c); if(a==2) cout<<(sum(c)-sum(b-1))<<endl; } return 0; }
我们现在来考虑第三个问题,也就是单点区间更新,单点查询;暴力做法就是在修改区间内的数一个一个修改,但这样的复杂度显然有点高,我们怎样能够通过树状数组来实现这个操作呢?我们联想一下普通数组的区间更新,区间查询问题,我们当时是构造的差分数组,同样的,我们在这里也可以构造一个差分数组d[],那么d[n]不就表示a[n]-a[n-1]了吗,那么c[n]=d[1]+d[2]+d[3]+....+d[n]=a[1]+(a[2]-a[1])+(a[3]-a[2])+....+(a[n]-a[n-1])=a[n],也就是说我们单点查询的结果就是d数组的前缀和,也就是对应的a数组的值。下面给出一道例题:(纯模板)
如题,已知一个数列,你需要进行下面两种操作:
-
将某区间每一个数数加上 xx;
-
求出某一个数的值。
输入格式
第一行包含两个整数 NN、MM,分别表示该数列数字的个数和操作的总个数。
第二行包含 NN 个用空格分隔的整数,其中第 ii 个数字表示数列第 ii 项的初始值。
接下来 MM 行每行包含 22 或 44个整数,表示一个操作,具体如下:
操作 11: 格式:1 x y k 含义:将区间 [x,y][x,y] 内每个数加上 kk;
操作 22: 格式:2 x 含义:输出第 xx 个数的值。
输出格式
输出包含若干行整数,即为所有操作 22 的结果。
输入输出样例
5 5 1 5 4 2 3 1 2 4 2 2 3 1 1 5 -1 1 3 5 7 2 4
6 10
下面是代码
#include<iostream> using namespace std; int a[500010],c[500010]; int n,m; int lowbit(int x) { return x&(-x); } void update(int x,int k) { while(x<=n) { c[x]+=k; x+=lowbit(x); } } int sum(int i) { int res=0; while(i>0) { res+=c[i]; i-=lowbit(i); } return res; } int main() { cin>>n>>m; for(int i=1;i<=n;i++) { cin>>a[i]; update(i,a[i]-a[i-1]);//我们所构造的是差分数组 } int a,b,c,d; while(m--) { cin>>a; if(a==1) { cin>>b>>c>>d; update(b,d);//更新数组左边界 update(c+1,-d);//更新数组右边界
} if(a==2) { cin>>c; cout<<sum(c)<<endl; } } return 0; }
最后一个问题就是区间更新区间查询了,这个问题我们又应该如何构造树状数组呢?这个呢我们还是利用差分的思想,有一些符号我还不会打,分析过程我就写在纸上了,哈哈,下面给大家附上图片:

例题找不到了,只能给出大家板子了
#include<iostream> using namespace std; int a[500010],c[500010],d[500010]; int n,m; int lowbit(int x) { return x&(-x); } void update(int x,int k) { int t=x-1; while(x<=n) { c[x]+=k;//维护差分数组 d[x]+=t*k;//维护(i-1)*d[i] x+=lowbit(x); } } int sum(int i)//求和 { int res=0,x=i; while(i>0) { res+=x*c[i]-d[i]; i-=lowbit(i); } return res; } int main() { cin>>n>>m; for(int i=1;i<=n;i++) { cin>>a[i]; update(i,a[i]-a[i-1]); } int a,b,c,d; while(m--) { cin>>a; if(a==1)//在b~c区间上加上d { cin>>b>>c>>d; update(b,d); update(c+1,-d); } if(a==2)//输出b~c区间的和 { cin>>b>>c; cout<<sum(c)-sum(b-1)<<endl; } } return 0; }
总结:树状数组功能性不如线段树强,但它的代码比较简单,可用于解决很多关于区间上的基础问题。
码了近三个小时,总算是码完了,码字不易,如果能够帮助到大家的话,希望大家能够动动手点个赞再走,谢谢啦~


