位运算

相信大家都知道在计算机内部存储的信息都是由0和1组成的，我们日常生活中所进行的加减乘除也都会转化到0和1上来进行运算，那么位运算有哪些优良性质呢？

位运算是计算机内部相对较为底层的东西了，越底层的东西，进行一些运算速度也会更快。比如我们要进行a*2我们完全可以通过a<<1来实现，虽然两者结果一样，但速度却有着很大的差别。

现在给出一些常见的位运算操作：

（1）取出整数n在二进制表示下的第k位（n>>k）&1;

（2）取出整数n在二进制下表示的第0~k-1位 n&( (1<<k) - 1 )

（3）把整数n在二进制表示下的第k位取反 n ^ ( 1<<k )

（4）对整数n在二进制表示下的第k位赋值1 n | =1<<k

(5) 对整数n在二进制表示下的第k位赋值0 n&( ~( 1<<k ) )

我今天所要介绍的优良性质是位运算在二进制表示下不进位，例如若ans=a&b,则ans的第k位只于a的第k位和b的第k位有关，而与其他位无关。

接下来以一道经典位运算题目来说明这个性质的用法

$21$

作为一名青春阳光好少年，atm 一直坚持与起床困难综合症作斗争。

通过研究相关文献，他找到了该病的发病原因：在深邃的太平洋海底中，出现了一条名为 drd 的巨龙，它掌握着睡眠之精髓，能随意延长大家的睡眠时间。

正是由于 drd 的活动，起床困难综合症愈演愈烈，以惊人的速度在世界上传播。

为了彻底消灭这种病，atm 决定前往海底，消灭这条恶龙。

历经千辛万苦，atm 终于来到了 drd 所在的地方，准备与其展开艰苦卓绝的战斗。

drd 有着十分特殊的技能，他的防御战线能够使用一定的运算来改变他受到的伤害。

具体说来，drd 的防御战线由

每扇防御门包括一个运算

如果还未通过防御门时攻击力为

最终 drd 受到的伤害为对方初始攻击力

由于 atm 水平有限，他的初始攻击力只能为

为了节省体力，他希望通过选择合适的初始攻击力使得他的攻击能让 drd 受到最大的伤害，请你帮他计算一下，他的一次攻击最多能使 drd 受到多少伤害。

输入格式

第

接下来

输出格式

输出一个整数，表示 atm 的一次攻击最多使 drd 受到多少伤害。

数据范围

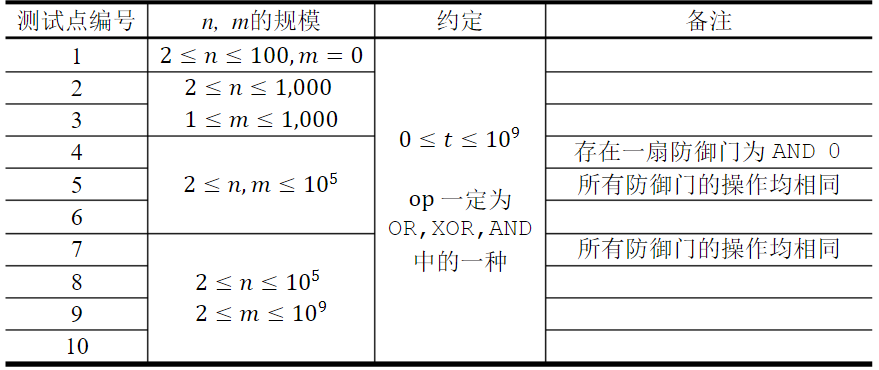
输入样例：

3 10
AND 5
OR 6
XOR 7

输出样例：

1

题目分析：看到这个题我们的第一思路应该会是暴力求解，把0到m个数全部遍历一遍，在遍历过程中更新最大值，但这种做法的复杂度是比较高的，肯定会被卡爆，我们不妨换种思考方式：
我们考虑最优解各个二进制数位，因为每个二进制数位只与与他进行运算的那个数的对应位置有关，所以我们不妨处理每一个二进制数位，以此来构造最优解。这道题我们还需要用到贪心思想，
考虑m的第k位的取值情况对于ans的第k位的影响，若m第k位可以为1，也就是若第k位为1，则所构造的数小于等于m，同时第k位为1运算所得结果比第k位为0运算结果大，那么我们就令第k位为1，
如果不满足同时这两种情况，则说明有可能是当第k位为1时，所构造数值超过m，则我们只能令他第k位数值位为0，也可能是第k位数值为0，则所得结果对应的第k位数值大于等于m的第k位数值为1时所
对应的第k位的值，本着贪心的原则，我们都应该让所构造数的第k位为0，分析到这就结束了，下面给大家附上代码：

#include<bits/stdc++.h>
using namespace std;
pair<string,int> a[100002];
int n,m;
int fun(int bit,int x)
{
    for(int i=1;i<=n;i++)
    {
        int temp=a[i].second>>bit&1;//取出每扇门的值的第k位二进制数
        if(a[i].first=="AND") x&=temp;
        else if(a[i].first=="OR") x|=temp;
        else if(a[i].first=="XOR") x^=temp;
    }
    return x;
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>a[i].first>>a[i].second;
    int ans=0,maxx=0;
    for(int i=30;i>=0;i--)
        {
            int res1=fun(i,1);
            int res2=fun(i,0);
            if((maxx+(1<<i))<=m&&res1>res2)//一定要满足所构造数小于等于m
                {
                    maxx+=1<<i;//更新所构造数此时的值
                    ans+=1<<i;//更新答案此时的值
                }
                else
                    ans+=res2<<i;
        }
    cout<<ans;
    return 0;
}

posted @ 2021-04-11 22:36 AC--Dream 阅读(128) 评论(0) 编辑收藏举报

刷新页面返回顶部

位运算

输入格式

输出格式

输入样例：

输出样例：

公告