线性筛及其扩展应用

好久没写博客了。不过noip的努力一直没有停止过~
今天学习了线性筛的扩展，正好时间有空，就来写博客了

1.线性筛

线性筛思路还是比较简单，即保证每个数只被它最小的因数筛去一次，
先看裸的代码：

#include<bits/stdc++.h>
using namespace std;

const int maxn=1000010;
int pri[maxn],fl[maxn],Cnt;

void Find_pri(){
	fl[1]=true;
	for(int i=2;i<maxn;i++){
		if(!fl[i])pri[++Cnt]=i;
		for(int j=1;j<=Cnt && pri[j]*i<maxn;j++){
			fl[i*pri[j]]=1;
			if(i%pri[j]==0)
				break;
		}
	}
}

int main( ){
	int m,n,j,k,i;
	Find_pri();
	return 0;
}

不多讲了。

2.欧拉函数

欧拉函数表示方法为

$$\varphi(d)=\sum_{i=1}^{d-1}[gcd(i,d)==1]$$

它满足性质：

(具体证明就不写了~)
所以上代码

void Find_Pri(){
	fl[1]=phi[1]=true;
	for(int i=2;i<maxn;i++){
		if(!fl[i])
			pri[++cnt]=i,phi[i]=i-1,fl[i]=true;
		for(int j=1;j<=cnt && i*pri[j]<maxn;j++){
			fl[i*pri[j]]=true;
			if(i%pri[j]==0){
				phi[i*pri[j]]=phi[i]*pri[j];break;
			}
			phi[i*pri[j]]=phi[i]*(pri[j]-1);
		}
	}
}

3.线性筛与莫比乌斯函数
莫比乌斯函数是个奇怪的函数(好像只有莫比乌斯反演才会用到吧)。
它的定义式为

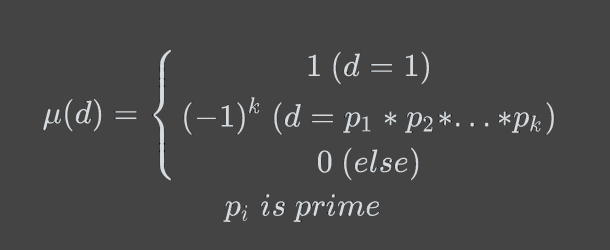
直接上代码：

#include<bits/stdc++.h>
using namespace std;

const int maxn=1000010;
int pri[maxn],fl[maxn],Cnt;
int mu[maxn];

void Find_pri(){
	fl[1]=mu[1]=1;
	for(int i=2;i<maxn;i++){
		if(!fl[i])pri[++Cnt]=i,mu[i]=-1;
		for(int j=1;j<=Cnt && pri[j]*i<maxn;j++){
			fl[i*pri[j]]=1;
			if(i%pri[j]==0){
				mu[i*pri[j]]=0;break;
			}
			mu[i*pri[j]]=mu[i]*-1;
		}
	}
}

int main( ){
	int m,n,j,k,i;
	Find_pri();
	return 0;
}

那么线性筛的基本应用就是这些