树的顺序遍历
树是一个优美的数据结构,在掌握了树的概念之后,首先需要知道的就是树的顺序遍历。
先序遍历
树的先序遍历是对于每一个子树(包括本身)以中(根节点)->右儿子->左儿子的顺序进行的遍历
void Build(){
printf("%d\n",root);
Build(lson);
Build(rson);
}
中序遍历
树的中序遍历是对于每一个子树(包括本身)以右儿子->中(根节点)->左儿子的顺序进行的遍历
void Build(){
Build(lson);
printf("%d\n",root);
Build(rson);
}
后序遍历
树的后序遍历是对于每一个子树(包括本身)以右儿子->左儿子->中(根节点)的顺序进行的遍历
void Build(){
Build(lson);
Build(rson);
printf("%d\n",root);
}
举个例子
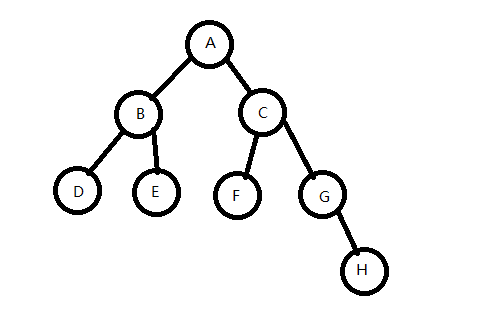
它的先序遍历是:ABDECFGH
它的中序遍历是:DBEAFCGH
它的后序遍历是:DEBFHGCA
观察后不难发现,树的顺序遍历有一些小性质:
先序遍历中的第一个一定是它的根节点,并且依次跟着它的左、右子树(对于它的子树也是如此)
后序遍历中的最后一个一定是它的根节点,并且依次跟着它的右、左子树(对于它的子树也是如此)
中序遍历中,某棵子树(在该子树范围内)的左边的一定是他左子树,右边的一定是它的右子树
现在先看一个题
题目链接
[USACO]奶牛血统
描述
农夫约翰非常认真地对待他的奶牛们的血统。然而他不是一个真正优秀的记帐员。他把他的奶牛们的家谱作成二叉树,并且把二叉树以更线性的“树的中序遍历”和“树的前序遍历”的符号加以记 录而不是用图形的方法。
你的任务是在被给予奶牛家谱的“树中序遍历”和“树前序遍历”的符号后,创建奶牛家谱的“树的后序遍历”的符号。每一头奶牛的姓名被译为一个唯一的字母。(你可能已经知道你可以在知道树的两种遍历以后可以经常地重建这棵树。)显然,这里的树不会有多于26个的顶点。 这是在样例输入和样例输出中的树的图形表达方式:
C
/ \
/ \
B G
/ \ /
A D H
/ \
E F
树的中序遍历是按照左子树,根,右子树的顺序访问节点。
树的前序遍历是按照根,左子树,右子树的顺序访问节点。
树的后序遍历是按照左子树,右子树,根的顺序访问节点。
格式
PROGRAM NAME: heritage
INPUT FORMAT:
(file heritage.in)
第一行: 树的中序遍历
第二行: 同样的树的前序遍历
OUTPUT FORMAT:
(file heritage.out)
单独的一行表示该树的后序遍历。
SAMPLE INPUT
ABEDFCHG
CBADEFGH
SAMPLE OUTPUT
AEFDBHGC
这道题明显是给出树的中序遍历与先序遍历求后序遍历,我们利用中序遍历左边为左儿子,右边为右儿子的性质来递归处理
不过记住:
树的先序遍历是对于每一个子树(包括本身)以中(根节点)->右儿子->左儿子的顺序进行遍历
void Build(){
printf("%d\n",root);
Build(lson);
Build(rson);
}
先序遍历的第一个一定是它的根节点,并且依次跟着它的左、右子树(对于它的子树也是如此)
上代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=200;
char fir[maxn],mid[maxn],las[maxn];
int len;
int Get(char* C){
int h=0;char Ch=getchar();
for(;Ch!='\n' && Ch!=EOF;Ch=getchar())
if(isgraph(Ch))C[h++]=Ch;
return h;
}
void Build(int l,int r){
int k=-1;if(l>r)return ;
for(int i=0;i<len;i++){\\先序遍历中,前面的一定是父亲
for(int j=l;j<=r;j++){
if(fir[i]==mid[j]){
k=j;break;
}
}
if(k!=-1)break;
}
Build(l,k-1);
Build(k+1,r);
putchar(mid[k]);
}
int main( ){
int m,n,j,k,i;
len=Get(mid);Get(fir);
Build(0,len-1);
puts("");
return 0;
}
这里还可以优化,就是建树的时候同时维护一下先序遍历的指针,使复杂度降为O(n)
#include<bits/stdc++.h>
using namespace std;
const int maxn=200;
char fir[maxn],mid[maxn],las[maxn];
int len;
int Get(char* C){
int h=0;char Ch=getchar();
for(;Ch!='\n' && Ch!=EOF;Ch=getchar())
if(isgraph(Ch))C[h++]=Ch;
return h;
}
void Build(int lx,int rx,int ly,int ry){
int k;
for(int i=lx;i<=rx;i++){
if(mid[i]==fir[ly]){
k=i;break;
}
}
if(k>lx)Build(lx,k-1,ly+1,ly-lx+k);
if(k<rx)Build(k+1,rx,ly-lx+k+1,ry);
putchar(mid[k]);
}
int main( ){
int m,n,j,k,i;
len=Get(mid);Get(fir);
Build(0,len-1,0,len-1);
puts("");
return 0;
}
另外其实给出后序遍历与中序遍历求先序遍历也差不多
注意建树时循环要倒过来(后序遍历后面的才是父亲)
#include<bits/stdc++.h>
using namespace std;
const int maxn=200;
char fir[maxn],mid[maxn],las[maxn];
int len;
void Build(int l,int r){
int k=0;
if(l>r)return ;
for(int i=len-1;i>=0;i--){
for(int j=l;j<=r;j++){
if(las[i]==mid[j]){
k=j;break;
}
}
if(k)break;
}
printf("%c",mid[k]);
Build(l,k-1);Build(k+1,r);
}
int Get(char* C){
int h=0;char Ch=getchar();
for(;Ch!='\n' && Ch!=EOF;Ch=getchar())
if(isgraph(Ch))C[h++]=Ch;
return h;
}
int main( ){
int m,n,j,k,i;
len=Get(mid);
Get(las);
Build(0,len-1);
puts("");
return 0;
}
优化:
#include<bits/stdc++.h>
using namespace std;
const int maxn=200;
char fir[maxn],mid[maxn],las[maxn];
int len;
int Get(char* C){
int h=0;char Ch=getchar();
for(;Ch!='\n' && Ch!=EOF;Ch=getchar())
if(isgraph(Ch))C[h++]=Ch;
return h;
}
void Build(int lx,int rx,int ly,int ry){
int k;
for(int i=lx;i<=rx;i++){
if(mid[i]==las[ry]){
k=i;break;
}
}
putchar(mid[k]);
if(k>lx)Build(lx,k-1,ly,ly-lx+k-1);
if(k<rx)Build(k+1,rx,ly-lx+k,ry-1);
}
int main( ){
int m,n,j,k,i;
len=Get(mid);Get(las);
Build(0,len-1,0,len-1);
return 0;
}
以上就是树的顺序遍历的基础~
但是,树的遍历看起来简单,但题目思维难度不小,具体参见此处



