软件工程第3次作业

软件工程第三次作业

1.题目

给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
-- 引用自《百度百科》

2.方法

此次采用线性时间算法，下为其他算法描述。

1）分治法算法描述如下

针对最大子段和这个具体问题本身的结构，我们还可以从算法设计的策略上对上述O(n^2)计算时间算法进行更进一步的改进。从问题的解结构也可以看出，它适合于用分治法求解。
如果将所给的序列a[1:n]分为长度相等的两段a[1:n/2]和a[n/2+1:n],分别求出这两段的最大子段和，则a[1:n]的最大子段和有三种情况：
（1） a[1:n]的最大子段和与a[1:n/2]的最大子段和相同
（2） a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同
（3） a[1:n]的最大子段和为a[i]+…+a[j]，并且1<=i<=n/2，n/2+1<=j<=n。
对于（1）和（2）两种情况可递归求得，但是对于情况（3），容易看出a[n/2]，a[n/2+1]在最大子段中。因此，我们可以在a[1:n/2]中计算出s1=max(a[n/2]+a[n/2-1]+…+a[i]),0<=i<=n/2，并在a[n/2+1:n]中计算出s2= max(a[n/2+1]+a[n/2+2]+…+a[i])，n/2+1<=i<=n。则s1+s2为出现情况（3）的最大子段和。

2）动态规划法如下

在对于上述分治算法的分析中我们注意到，若记b[j]=max(a[i]+a[i+1]+..+a[j]),其中1<=i<=j,并且1<=j<=n。则所求的最大子段和为max b[j]，1<=j<=n。
由b[j]的定义可易知，当b[j-1]>0时b[j]=b[j-1]+a[j]，否则b[j]=a[j]。故b[j]的动态规划递归式为:
b[j]=max(b[j-1]+a[j],a[j])，1<=j<=n。

3.线性时间算法代码

public class Add3 {
int MaxSubSum3(int[] arr,int len)
{
    int i;
    int MaxSum = 0;
    int CurSum = 0;
    for(i=0;i<len;i++)
    {
        CurSum += arr[i];
        if(CurSum > MaxSum)
            MaxSum = CurSum;
        if(CurSum < 0)
            CurSum = 0;
    }
    return MaxSum;
}


}

4.单元测试

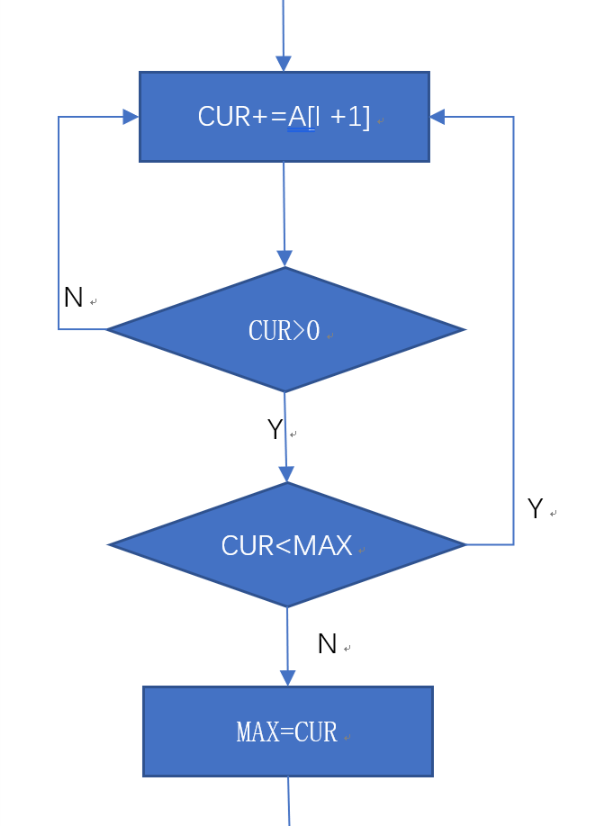
采用条件组合覆盖，由图可知只有三种情况需要考虑；
即 NNN...
YYY...
Y...YN 三种情况
本只需两个测试用例即可全部覆盖（testMaxSubSum3 & testMaxSubSum7），此次列出了尽可能多的测试用例，
详情见测试代码。

5.测试代码

import static org.junit.Assert.*;

import org.junit.Test;

public class Add3Test {

@Test
public void testMaxSubSum3() {
	int[] arr = new int[]{1,2,3,4,5,6};
	int sum = new Add3().MaxSubSum3(arr, 6);		
	assertEquals(21,sum);
}

@Test
public void testMaxSubSum4() {
	int[] arr = new int[]{-1,-2,-3,4,-5,-6};
	int sum = new Add3().MaxSubSum3(arr, 6);		
	assertEquals(4,sum);
}

@Test
public void testMaxSubSum5() {
	int[] arr = new int[]{0,2,3,14,-15,16};
	int sum = new Add3().MaxSubSum3(arr, 6);		
	assertEquals(20,sum);
}

@Test
public void testMaxSubSum6() {
	int[] arr = new int[]{0,0,18,0,0,-6};
	int sum = new Add3().MaxSubSum3(arr, 6);		
	assertEquals(18,sum);
}

@Test
public void testMaxSubSum7() {
	int[] arr = new int[]{-1,-2,-3,-4,-5,-6};
	int sum = new Add3().MaxSubSum3(arr, 6);		
	assertEquals(0,sum);
}

6.测试结果

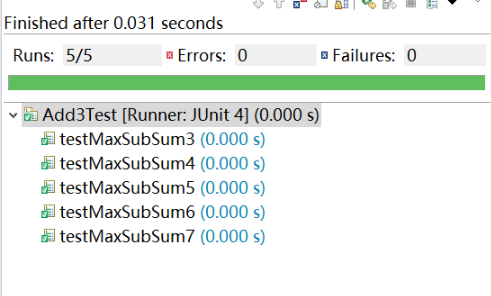
小结

通过这次作业，越发熟练起来进行单元测试了！
大量时间并没有花费在编写代码上！

代码地址：https://coding.net/u/A1675845/p/15GradeSoftEngin/git?public=true