思路来自 这里。
\(\operatorname{fib}(1)=\operatorname{fib}(2)=1,\operatorname{fib}(n)=\operatorname{fib}(n-1)+\operatorname{fib}(n-2),n\ge 3\)
那么：
\(\sum\limits_{i=1}^n \operatorname{fib}^2(i)=\operatorname{fib}(n)\operatorname{fib}(n+1)\)
可以考虑一下几何意义证明，\(n\) 个正方形拼成一个大矩形。
代数：
\[\begin{aligned}
&\operatorname{fib}(n)\operatorname{fib}(n+1)-\operatorname{fib}(n-1)\operatorname{fib}(n)\\
&=\operatorname{fib}(n)[\operatorname{fib}(n)+\operatorname{fib}(n-1)]-\operatorname{fib}(n-1)\operatorname{fib}(n)\\
&=\operatorname{fib}^2(n)
\end{aligned}
\]
累加即可。
\(\sum\limits_{i=1}^n\operatorname{fib}^2(i)\operatorname{fib}(i+1)=\frac{\operatorname{fib}(n)\operatorname{fib}(n+1)\operatorname{fib}(n+2)}{2}\)
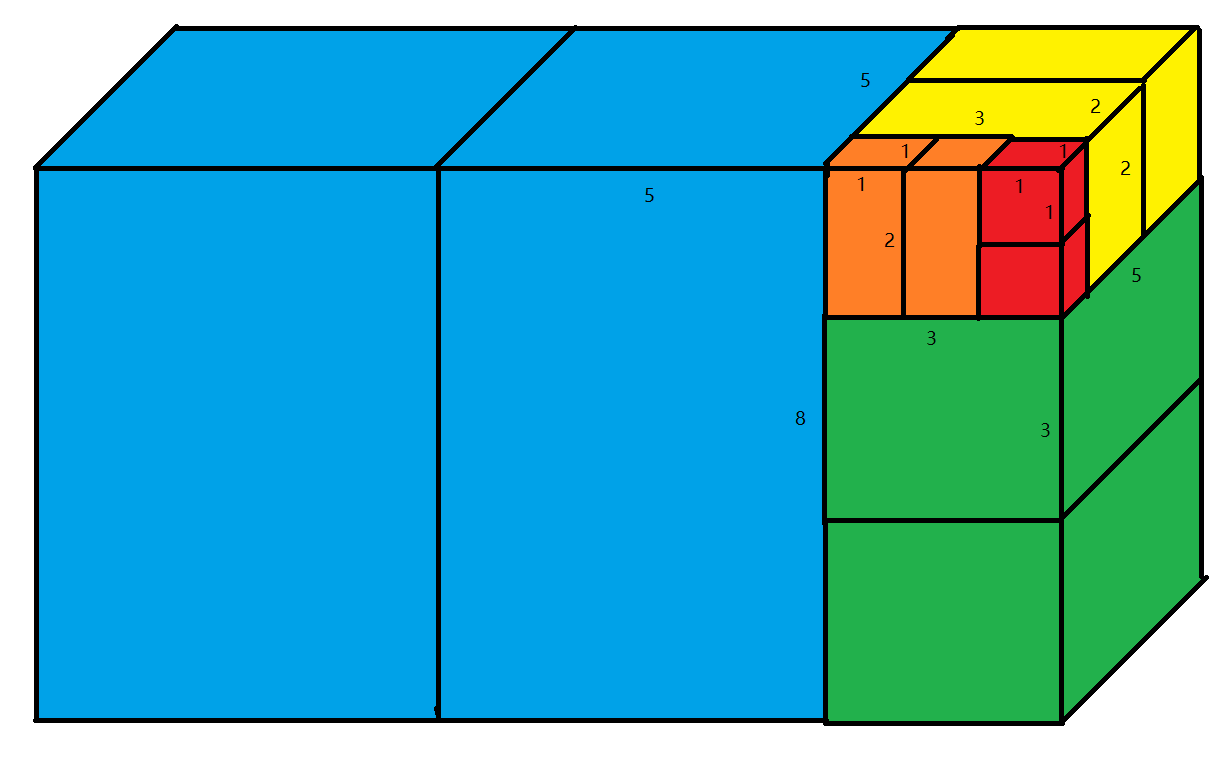
这个也是可以证明的，同样利用立体几何法：
图片请勿自行转载，转载请标明出处
利用了 \(\operatorname{fib}(n)=2\operatorname{fib}(n-2)+\operatorname{fib}(n-3)\)。
依次在 左，后，下，左，后，下……放长方体即可。
代数：
\[\begin{aligned}
&\operatorname{fib}(n)\operatorname{fib}(n+1)\operatorname{fib}(n+2)-\operatorname{fib}(n-1)\operatorname{fib}(n)\operatorname{fib}(n+1)\\
&=\operatorname{fib}(n)\operatorname{fib}(n+1)[2\operatorname{fib}(n)+\operatorname{fib}(n-1)]-\operatorname{fib}(n-1)\operatorname{fib}(n)\operatorname{fib}(n+1)\\
&=2\operatorname{fib}^2(n)\operatorname{fib}(n+1)
\end{aligned}
\]
累加即可。
更高次数的不会很好看：
\[\begin{aligned}
&\operatorname{fib}(n)\operatorname{fib}(n+1)\operatorname{fib}(n+2)\operatorname{fib}(n+3)-\operatorname{fib}(n-1)\operatorname{fib}(n)\operatorname{fib}(n+1)\operatorname{fib}(n+2)\\
&=\operatorname{fib}(n)\operatorname{fib}(n+1)\operatorname{fib}(n+2)[\operatorname{fib}(n-1)+\operatorname{fib}(n)+\operatorname{fib}(n+2)]-\cdots\\
&=\operatorname{fib}(n)\operatorname{fib}(n+1)\operatorname{fib}(n+2)[\operatorname{fib}(n)+\operatorname{fib}(n+2)]\\
&=\operatorname{fib}(n)[\operatorname{fib}(n)+\operatorname{fib}(n-1)][\operatorname{fib}(n)+\operatorname{fib}(n+1)][\operatorname{fib}(n)+\operatorname{fib}(n+2)]\\
&=\frac{1}{2}[\operatorname{fib}(n)+\operatorname{fib}(n-1)][\operatorname{fib}(n)+\operatorname{fib}(n)][\operatorname{fib}(n)+\operatorname{fib}(n+1)][\operatorname{fib}(n)+\operatorname{fib}(n+2)]\\
\end{aligned}
\]
其他性质：
-
杨辉三角的斜对角求和；
-
\(\operatorname{fib}(n-1)\operatorname{fib}(n+1)-\operatorname{fib}^2(n)=(-1)^n\)；
-
\(\operatorname{fib}(1)+\operatorname{fib}(3)+\cdots +\operatorname{fib}(2n-1)=\operatorname{fib}(2n)\)；
-
\(\operatorname{fib}(2)+\operatorname{fib}(4)+\cdots +\operatorname{fib}(2n)=\operatorname{fib}(2n+1)-1\)；
-
\(\frac{\operatorname{fib}(2n)}{\operatorname{fib}(n)}=\operatorname{fib}(n-1)+\operatorname{fib}(n+1)\)。
