BZOJ 1800飞行棋题解--zhengjun
Description
给出圆周上的若干个点,已知点与点之间的弧长,其值均为正整数,并依圆周顺序排列。 请找出这些点中有没有可以围成矩形的,并希望在最短时间内找出所有不重复矩形。
Input
第一行为正整数\(N\),表示点的个数,接下来\(N\)行分别为这\(N\)个点所分割的各个圆弧长度
Output
所构成不重复矩形的个数
Sample Input
8
1
2
2
3
1
1
3
3
Sample Output
3
HINT
\(N<= 20\)
思路
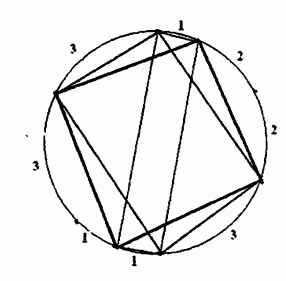
看图可知,每一个长方形相对的点在圆弧上总是处于同一条直径上(就是在对面),样例就一共有3组(1和5,2和6,4和8),而矩形需要两条对角线,也就是两组相对的点,因为不能重复,所以就是3个选2个的组合,一共有3个,答案就出来了!
代码
#include<bits/stdc++.h>
using namespace std;
inline void read(int &x)//我爱快读
{
x=0;register char c=getchar();
while(c<'0'||c>'9'){c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
}
int n;
int f[1000039],a[50],ans,sum=0;
int main()
{
read(n);
for(int i=1;i<=n;i++)
{
read(a[i]);
sum+=a[i];
f[a[i]=sum]=1;
}
for(int i=1;i<=n;i++)
{
if(a[i]<=sum/2&&f[sum/2+a[i]])//防止重复计算
ans++;
}
cout<<(ans-1)*ans/2;//组合函数
return 0;
}



