Uva_11235_Frequent values

T^T做这题就是各种泪~卡了将近2小时，各种Judging error、越界与WA。

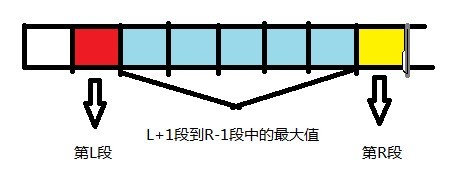
题解：整个数组是非降序的，所有相等元素都会聚集在一起。开一个num数组，用num[i]来记录第i段相等的元素有多少个（也就是说相当于RMQ中的元素值了），num数组的长度就是原数列不同元素的个数（段数）,l数组记录i段元素的上界，r数组记录i段元素的下界，用一个mark数组记录i位置的元素属于第几段。假设询问区间为a,b：

L=mark[a],R=mark[b];

ans=max(r[L]-a+1,b-l[R]+1，夹在这两个段中最大值)

图解：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
using namespace std;
#define N 100005
int mark[N],val,num[N],l[N],r[N],maxsum[N][25],re; //mark记录i位置的元素是第几段
void RMQ()
{
    for(int i=1;i<=re;++i)
    maxsum[i][0]=num[i];
    for(int j=1;(1<<j)<=re+1;++j)
        for(int i=1;i+(1<<j)-1<=re;++i)
            maxsum[i][j]=max(maxsum[i][j-1],maxsum[i+(1<<(j-1))][j-1]);
}
int Max(int a,int b,int c)
{
    if(a<b) a=b;
    if(a<c) a=c;
    return a;
}
int main(){
  int n,q,i,j,k,L,R;
  while(~scanf("%d",&n)&&n)
  {
      re=1; //re记录的是第几段
      scanf("%d%d",&q,&k);
      val=k;
      num[1]=1;
      mark[1]=1;
      l[0]=1;
      for(i=2;i<=n;++i)
      {
          scanf("%d",&k);
          if(k==val) 
          {
              num[re]++;
              mark[i]=re;
          }
          else
          {
              r[re]=i-1;
              re++;
              mark[i]=re;
              l[re]=i;
              val=k;
              num[re]=1;
          }
      }
      RMQ();
      while(q--)
      {
          scanf("%d%d",&L,&R);
          if(mark[L]==mark[R])
              printf("%d\n",R-L+1);
          else
          {
              int ans=0;
              if(mark[L]+1<=mark[R]-1) //如果两段中存在段
              {
              int k=(int)((log(mark[R]-mark[L]-1))/log(2.0));
               ans=max(maxsum[mark[L]+1][k],maxsum[mark[R]-(1<<k)][k]);
              }
               ans=Max(r[mark[L]]-L+1,ans,R-l[mark[R]]+1);
               printf("%d\n",ans);
          }
      }
  }
  return 0;
}