【题目-任务安排2】斜率优化dp

目录

• 题解

 

---

回到顶部

题解

• 首先，递推关系如下：
  $dp[i] = min(dp[i], dp[j] + sumt[i] * (sumc[i] - sumc[j]) + s * (sumc[n] - sumc[j]));$
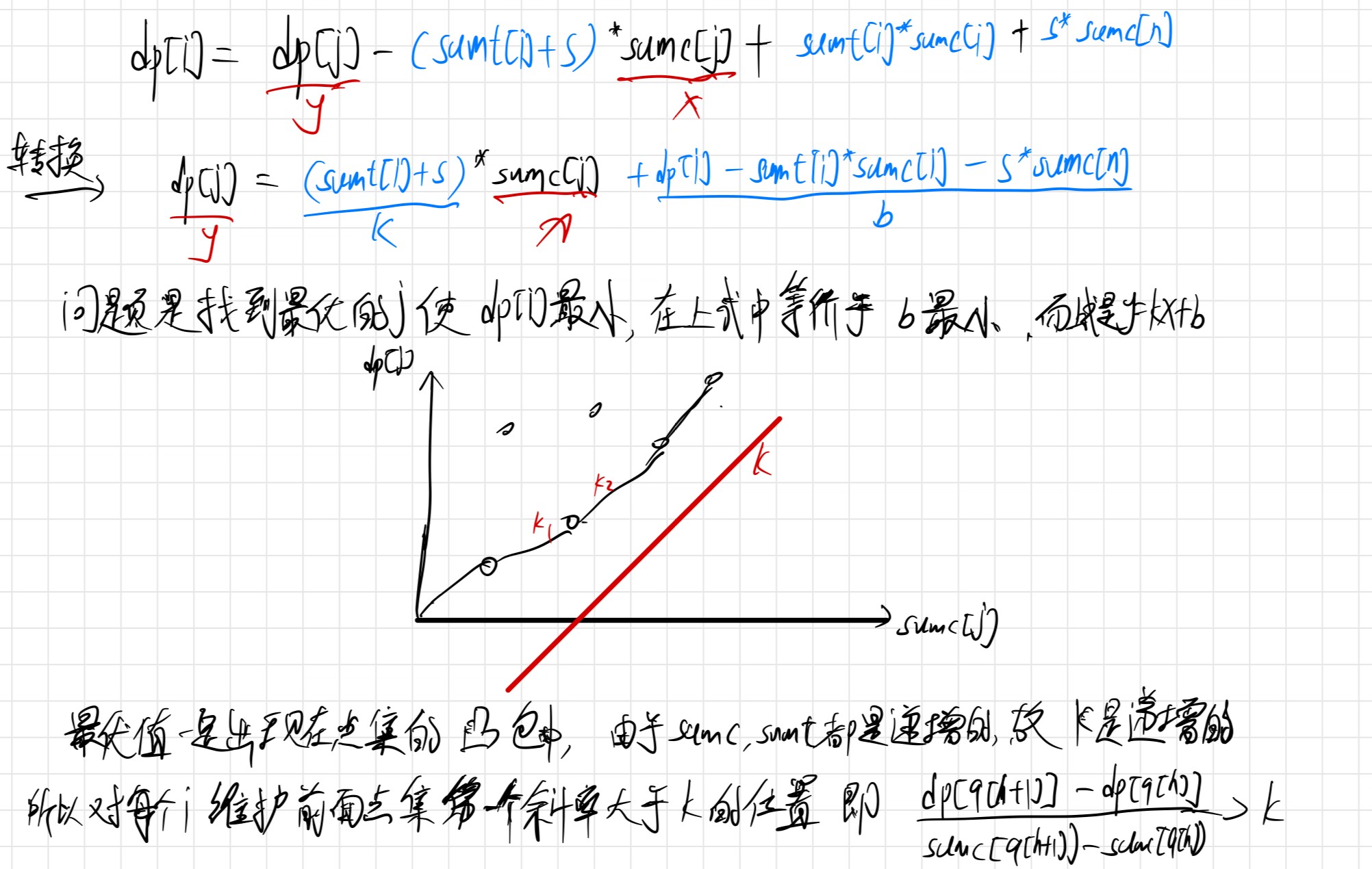
• 显然N太大，无法$O(n^2)$算法解决问题。考虑如何优化掉第二个j的循环，发现这个循环是找最优的j位置
• 假设$j$就是最优位置，那么可以先初步消掉min，接着如下分析：
• 
• 

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 3e5 + 5;

typedef long long ll;

ll dp[N];
ll sumt[N], sumc[N];

int q[N];

int main() {
    int n; ll s; scanf("%d%lld",&n, &s);
    for(int i = 1; i <= n; ++ i) {
        ll t, c; scanf("%lld%lld", &t, &c);
        sumt[i] = sumt[i - 1] + t;
        sumc[i] = sumc[i - 1] + c;
    }
    int h = 0, t = -1;
    
    for(int i = 1; i <= n; ++ i) dp[i] = 1e18;
    dp[0] = 0;
    
    q[++ t] = 0;
    for(int i = 1; i <= n; ++ i) {
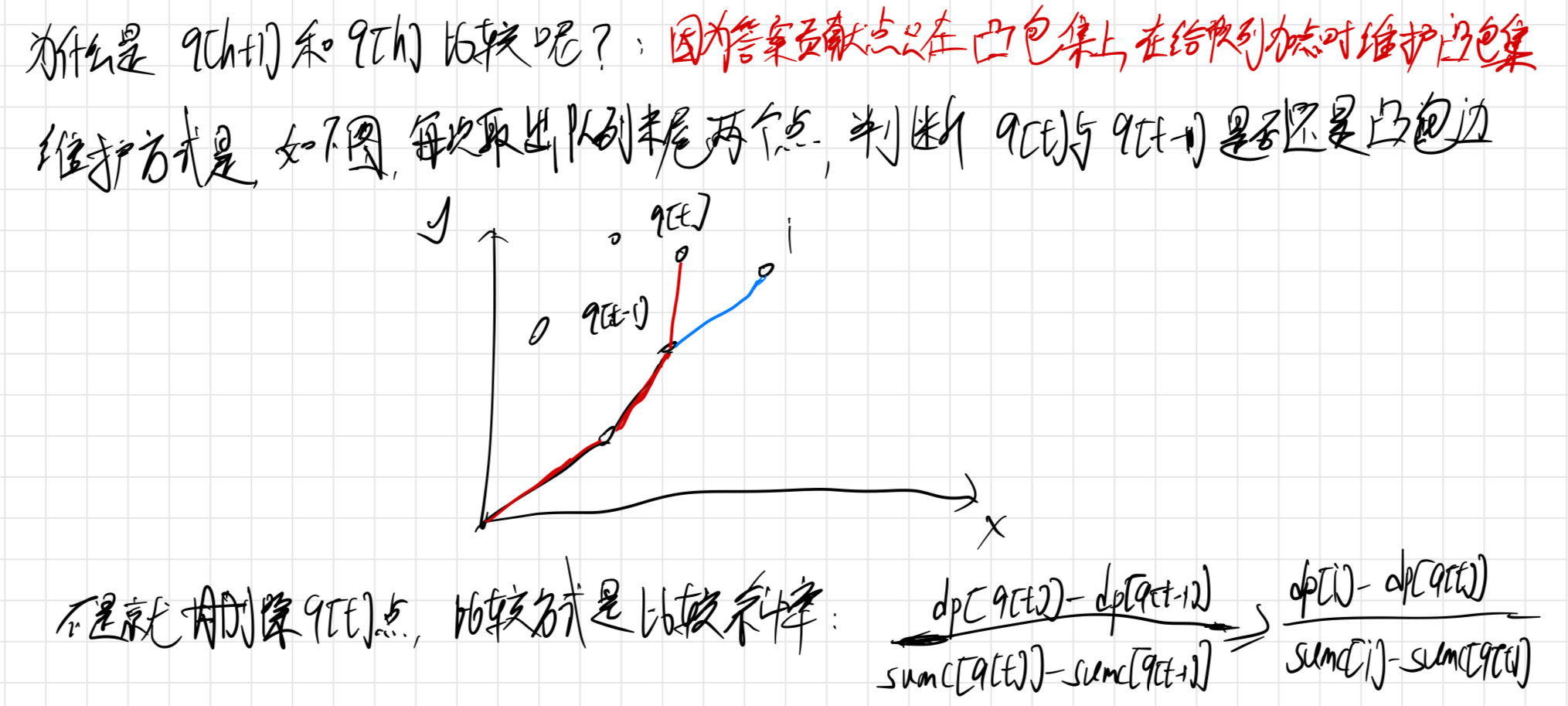
        while(h < t && dp[q[h + 1]] - dp[q[h]] <= (sumt[i] + s) * (sumc[q[h + 1]] - sumc[q[h]])) h ++;
        dp[i] = dp[q[h]] + sumt[i] * (sumc[i] - sumc[q[h]]) + s * (sumc[n] - sumc[q[h]]);
        while (h < t && (dp[q[t]] - dp[q[t - 1]]) * (sumc[i] - sumc[q[t - 1]]) >= (dp[i] - dp[q[t - 1]]) * (sumc[q[t]] - sumc[q[t - 1]])) t --;
        q[++ t] = i; 
    }
    printf("%lld\n", dp[n]);
    return 0;
}