E. Star MST (DP) (Educational Codeforces Round 125)

E. Star MST

Educational Codeforces Round 125 (Rated for Div. 2) E. Star MST

题目：

输入n, k。指n个点构成的完全无向图(完全图指任意两点间有一条边)，加权边取值为1~k之间，如果与1点相连的边的权值和与MST的权值和相等，则这样的图称为"美丽的"。问这样的图的数量。结果模 998244353。

题解：

学习自cf用户Heltion的解法。考虑dp[i][j]为i个点，取值在1~k之间的满足要求图数量。它的转移如下：

\[dp[i][j] = \sum_{z = 1}^{i} dp[z][j-1]*C_{i-1}^{z-1}*(k-j+1)^{[(z-1)*(i-z) + (i-z)*(i-z+1)/2]} \]

解释一下：就是现在已经有包括1点在内的z个点数量求出来了，考虑把剩下i - z个点和1连起来。这些点和1点连接的权值是j。\(C_{i-1}^{z-1}\) 表示除1点外剩余i-1个点中选z-1个点和1点构成已经求出结果的z个点。\([(z-1)*(i-z) + (i-z)*(i-z+1)/2]\)分别是除1外z-1个点和还未连进来的i-z个点之间连边数量，以及i-z个还未连进来的点之间连边的数量。由于这些边都不会影响结果，只要权值>=j就行，共(k-j+1)种取值。最后dp[n][k]就是答案

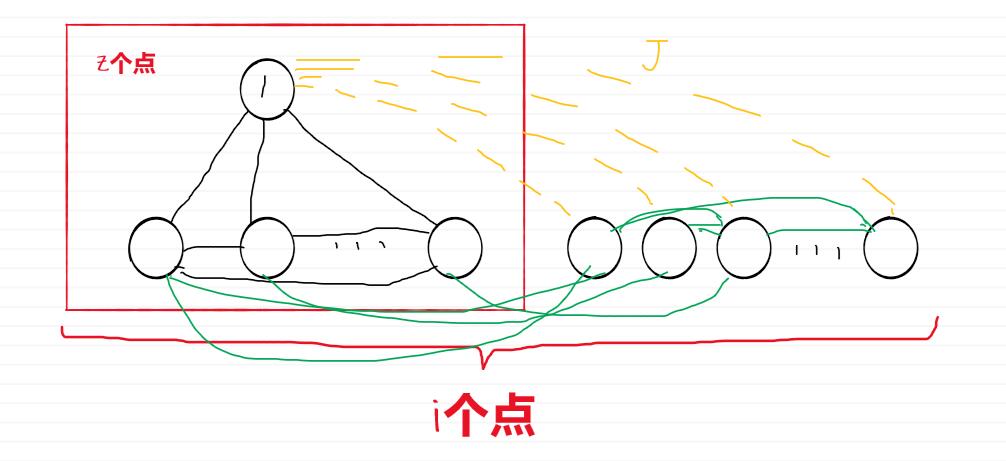
如图：黑色是已经连好的边，黄色是为了满足要求的权值为j的边，绿色是不影响结果的边。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#include<queue>
#include<cmath>
using namespace std;
typedef pair<double, int> PII;
typedef long long ll;
const int N = 1e3 + 5;
const ll mod = 998244353;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return !b ? a : gcd(b, a % b); }
ll lcm(ll a, ll b) { return a * b / gcd(a, b); }

ll n, k;
ll dp[N][N];

ll fac[N], inv[N];
void init(){
    fac[0] = inv[0] = 1;
    for(int i = 1; i < N; ++ i) fac[i] = fac[i - 1] * i % mod;
    inv[N - 1] = qpow(fac[N - 1], mod - 2);
    for(int i = N - 2; i >= 0; -- i) inv[i] = inv[i + 1] * (i + 1) % mod;
}

int main(){
    init();
    scanf("%lld%lld",&n, &k);
    dp[1][0] = 1;
    for(int i = 1; i <= n; ++ i){
        for(int j = 1; j <= k; ++ j){
            for(int z = 1; z <= i; ++ z){
                ll tp = dp[z][j - 1] * fac[i - 1] % mod * inv[z - 1] % mod * inv[i - z] % mod;
                ll tpp = qpow(k - j + 1, (z - 1) * (i - z) + (i - z) * (i - z - 1) / 2) % mod;
                dp[i][j] = (dp[i][j] + tp * tpp) % mod; 
            }
        }
    }
    printf("%lld\n",dp[n][k]);
    return 0;
}