Code forces E94 G.Mercenaries (容斥原理)

这道题也是看博客研究了1天。

参考博客

题意：

有n个士兵，第i个士兵只能参与大小在 \(l_{i}\) 到 \(r_{i}\) 的集合的构建。同时有m对仇恨关系，求构建无仇恨关系的集合数量。

题解：

用num[i]表示 可以参与组成大小为 i 的集合的士兵个数

首先如果不考虑任何限制，那么每个大小 k 的贡献就是：\(C_{num[k]}^{k}\) , 答案是\(\sum_{k=1}^{n}C_{num[k]}^{k}\) 。接着考虑限制的情况。每个限制由两个士兵组成, 设为x, y 。同样我们先考虑对应一个子集 S 的情况，那么就有四种情况：

• \(x \in S , y \in S\)
• \(x \in S, y \notin S\)
• \(x \notin S, y \in S\)
• \(x \notin S, y \notin S\)

按照题目要求，有矛盾的士兵不能在一个集合中，所以上面四种情况中除第一个以外其他都满足题意，对答案有贡献。但情况太多了不好算，我们按照 “正难则反” 的思想，去计算第一种情况的结果，在用总结果减去就是答案。

那如何计算第一种情况呢？

那问题转换成：士兵构成的集合存在矛盾的数量。

那这个集合可能存在第1对矛盾，也可能存在第2对矛盾，也可能同时存在1，2对矛盾。所以各情况可能存在重叠计算，这是容斥的经典模型。

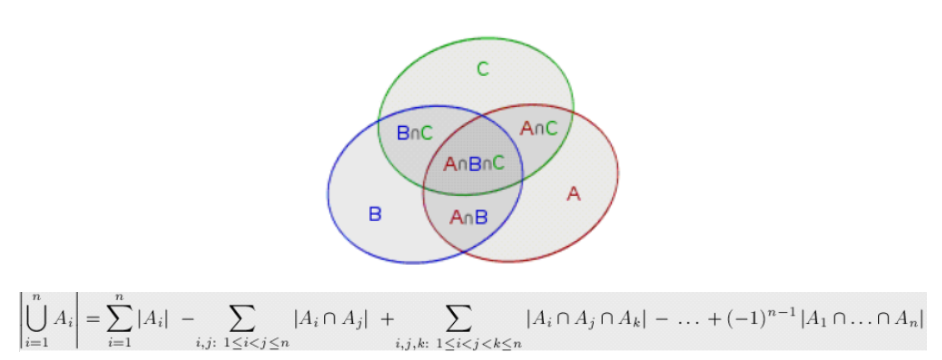
所以这个答案用容斥计算就是：

\[|\cup_{i=1}^{n}| = \sum_{t=1}^{m}(-1)^{t-1}\sum_{1\le i_{1}\lt i_{2}\lt...\lt i_{k}\le m}|A_{i_{1}} \cap A_{i_{2}}\cap ...\cap A_{i_{k}}| \]

最后再用不受限制的答案减去存在矛盾情况的答案，就是要的无矛盾的答案。因为不受限相当于t=0的答案，所以可以写为：

\[res = \sum_{t=0}^{m}(-1)^{t}\sum_{1\le i_{1}\lt i_{2}\lt...\lt i_{k}\le m}|A_{i_{1}} \cap A_{i_{2}}\cap ...\cap A_{i_{k}}| \]

具体实现：

\(sum[i][j]\) 用来表示构成大小为 j 的集合中有 i 个矛盾的点的方案数的前缀和。 之所以求前缀和主要是为了在容斥中，在d个矛盾的点时快速计算其在集合大小区间[l, r]之间的贡献值之和。那么\(sum[i][j] = sum[i][j - 1] + C_{num[j]-i}^{j-i}\)。

类比上面容斥的图，第 i 圈个表示包含第 i 个限制的情况集合。如果直接按照公式计算会发现这些圈的交集不好算。但是反过来对某一情况，去算它是含有几个限制好算。

但是我们发现m很小，所以这里我们状压m个限制选不选的情况。对每个情况计算矛盾点个数 d，以及这些点能参与构成的集合大小区间交集[L, R] ，只有这个区间内的集合大小才能出现这些矛盾点同时构成集合的情况。很容易用sum[] []数组计算出这个情况的贡献，公式：\(sum[d][R] - sum[d][L - 1]\) 。 如果共有奇数个限制就减，偶数个限制参与就加上答案。

代码：

//2020/8/28/14:06
//容斥原理

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<string>
#include<fstream>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i);
#define per(i, a, n) for(int i = n; i >= a; -- i);
typedef long long ll;
const int N = 3e5 + 10;
const int M = 5e3 + 10;
const int mod = 998244353;
const double Pi = acos(- 1.0);
const int INF = 0x3f3f3f3f;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
bool cmp(int a, int b){return a > b;}
//


int n, m;
int l[N], r[N], tx[N], ty[N]; ll num[N], fac[N], inv[N];
ll sum[50][N];


ll C(ll a, ll b){
    if(a < b || b < 0) return 0;
    return fac[a] * inv[b] % mod * inv[a - b] % mod;
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 1; i <= n; ++ i){
        scanf("%d%d",&l[i],&r[i]);
        num[l[i]] ++; num[r[i] + 1] --;
    }
    for(int i = 1;  i <= n; ++ i) num[i] = (num[i] + num[i - 1]) % mod;
    for(int i = 1; i <= m; ++ i) scanf("%d%d",&tx[i],&ty[i]);
    fac[0] = 1;
    for(ll i = 1; i < N; ++ i) fac[i] = fac[i - 1] * i % mod;
    inv[N - 1] = qpow(fac[N - 1], mod - 2);
    for(ll i = N - 2; i >= 0; -- i) inv[i] = inv[i + 1] * (i + 1) % mod;
    
    for(int i = 0; i <= m * 2; ++ i){
        for(int j = 1; j <= n; ++ j){
            sum[i][j] = (sum[i][j - 1] + C(num[j] - i, j - i)) % mod;
        }
    }
    
    ll res = 0;
    for(int i = 0; i < 1 << m; ++ i){
        set<int> st; int L = 1, R = n;
        for(int j = 0; j < m; ++ j){
            if((i >> j) & 1){
                int x = tx[j + 1], y = ty[j + 1];
                st.insert(x); st.insert(y);
                L = max(L, max(l[x], l[y])); 
                R = min(R, min(r[x], r[y]));
            }
        }
        int d = st.size();
        ll val = 0;
        if(L <= R) val = (sum[d][R] - sum[d][L - 1] + mod) % mod; 
        if(__builtin_popcount(i) & 1) res = (res - val + mod) % mod;
        else res = (res + val) % mod;
    }
    
    printf("%lld\n",res);
    return 0;
}