基环树 / 环套树
基环树 / 环套树
参考资料:
最近开始学基环树,思路不是很难但是实现有点难复杂,很考验基础能力。
什么是基环树:
如果一张无向连通图包含恰好一个环,则称它是一棵 基环树 。
如果一张有向弱连通图每个点的入度都为 1,则称它是一棵 基环外向树 。
如果一张有向弱连通图每个点的出度都为 1,则称它是一棵 基环内向树 。
多棵树可以组成一个 森林 (Forest) ,多棵基环树可以组成 基环森林 ,多棵基环外向树可以组成 基环外向树森林 ,多棵基环内向树可以组成 基环内向森林 (Functional graph) 。

如上图,基环树有 n 个点 n 条边,且环上每个点是一棵树的根结点。
基环树有哪些操作:
基环树经典的模型是:求基环树的直径,求基环树两点间的距离,基环树dp等。
当然它不过是一个稍特别的树,毕竟把环上一条边断开就变成树了。理解并不难,实现的话细节比较多。
如何处理基环树:
基环树 = 多个子树 + 环 (理解)
所以可以把处理基环树分成处理树和处理环两个步骤。
1)处理树:学习基环树,那基本的树的处理应该都会。处理树操作就是一些图论中树的基本操作。
2)处理环:
-
方法一:先找到环,把环上的点放进一个集合,根据性质环上点都是一个子树的根节点,所以可以遍历存环的集合,把基环树拆成许多子树,然后用1) 中处理树的方式把子树处理好,一般这样处理后这个环上的点都会得到一个权值 val[i] (具体根据题目定)。
然后问题就变成一个环,每个点都有权值,问你一些问题。 下面就是单纯的环的问题,把环断开复制一份接在后面去处理,具体见环形dp章节。通过题目< 岛屿> 理解。(这题居然是模板题,挺麻烦的。。)
-
方法二:基环树不过是在树的基础上连了一条边,使图多了个环,那我直接点,把环上一边断开变成树去处理。当然不能直接断,这条边加上对问题肯定有几种状态的影响,但毕竟只是一条边所以影响的状态不会很多,所以你可以断这条边,然后讨论这条边在时的状态。具体通过题目 <骑士>理解。
第一步:找环
找环是学会处理基环树的第一步!!!!
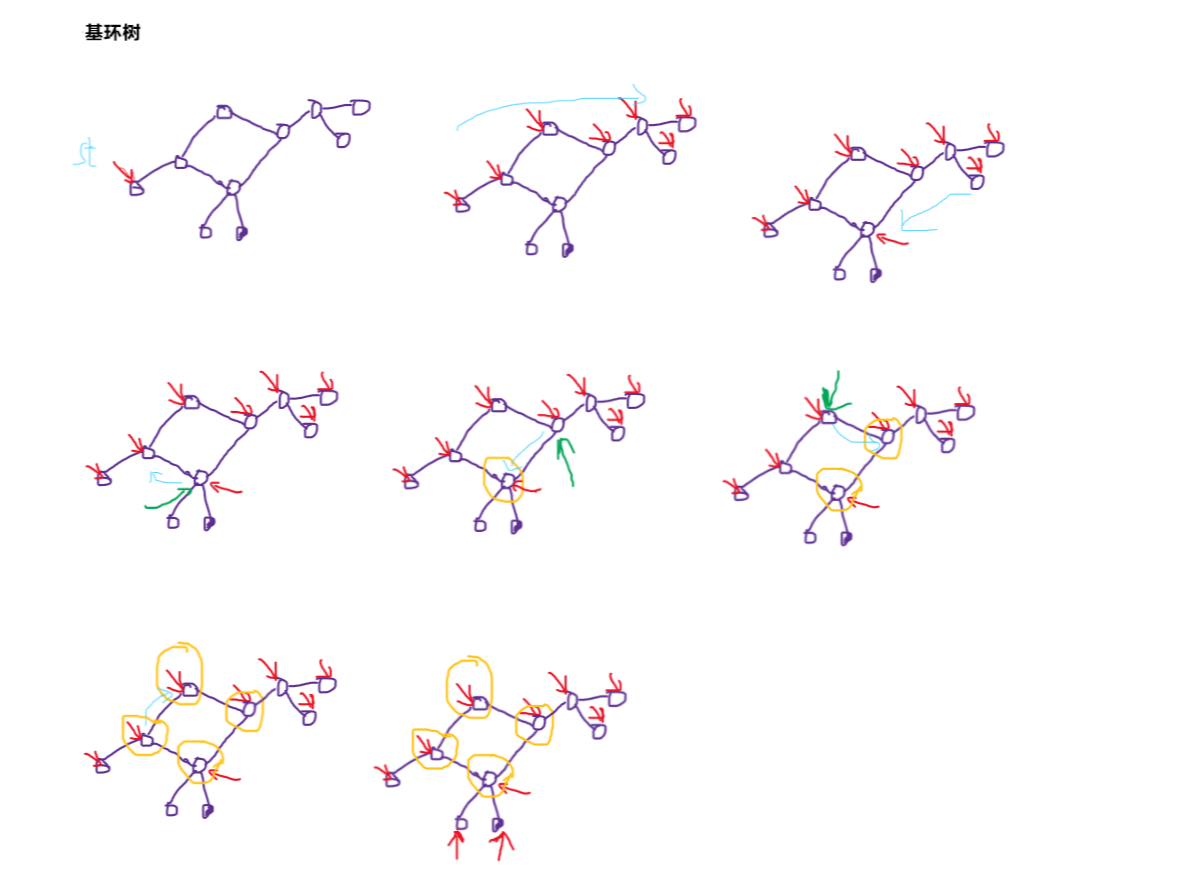
1)从一点开始遍历树
2)3)一直遍历树,并打标记
4)遍历到蓝箭头所指点时,发现这个点已经标记了,说明我们找到环了。所以先用绿箭头(代码中的now) 指向父亲节点,把绿箭头所指点放入存环的集合v中。
5)绿箭头沿着 蓝箭头(遍历的循序) 移动到指向刚放入v的点的父亲,把绿箭头指向的点放入v。
6)绿箭头沿着蓝箭头移动到上一个放入点父亲结点。把绿箭头指向的点放入v
7)直到绿箭头指向最初遇到的点时不在循环。把这个最初的点放入v中。标记flag表示已经处理了环,以后遇到"环"的情况就直接跳过,因为n个点n条边最多一个环。
8)继续处理其他点,直到所有点都被标记
//代码参考岛屿题解QwQ
void dfs(int u, int in_edge){
vis[u] = true;
for(int i = head[u]; i != -1; i = edge[i].nxt){
int v = edge[i].to, w = edge[i].c;
if((i ^ 1) == in_edge) continue;//指向父亲的边直接跳过
if(flag && vis[v]) continue; //后面遇到环直接跳过
if(vis[v]){ //第一次遇到环
int now = i ^ 1; //now就是绿箭头
while(edge[now].to != v){ //循环把所有点放进存环集合tv中
tv.push_back(PII(edge[now].to, edge[now].c));
mark[edge[now].to] = true;
now = fa[edge[now].to];
}
tv.push_back(PII(edge[now].to, edge[now].c));
mark[edge[now].to] = true;
flag = true;
continue;
}
fa[v] = i ^ 1;
dfs(v, i);
}
}


