Codeforces Round #568 (Div. 2)
Codeforces Round #568 (Div. 2)
D - Extra Element
这道题题的突破口就在这个"去掉一个值", 这说明你除了去掉的点其他点排序后相邻距离d是一样的。所以我们直接考虑这个d是多少,然后看能不能去掉一个点达到要求。显然不能枚举d,但是由于只去掉1个点,所以我们可以考虑3个情况(排序后):1) 去掉1点 2) 去掉2点 3)去掉其他点
去掉 1 点:
- 说明d = 2, 3两点之间的距离。 然后枚举检查其他点之间距离是不是等于d。由于已经去掉1点所以后面不考虑去点。
去掉2点:
- 说明d = 1, 3 两点之间的距离,然后枚举检查其他点之间的距离是不是等于d, 也不用考虑去点。
去掉其他点:
- 说明d = 1, 2两点之间的距离,由于还没有去点,所以要考虑去掉哪个点。
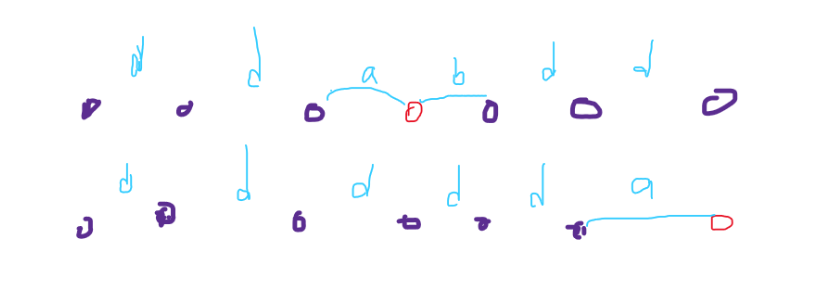
- 显然去掉的点有满足图中两种情况之一才有解:(红点表示去掉的点)
- 第一就是排序后有两个不等于 d 的距离a,b。 a + b = d, 且这两个点是相邻的。
- 第二就是只有一个不等于d的距离a,但是这个点在最后面。
代码:
#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i);
#define per(i, a, n) for(int i = n; i >= a; -- i);
#define px first
#define py second
typedef long long ll;
typedef pair<int,int> PII;
const int N = 4e5 + 5;
const int mod = 998244353;
const double Pi = acos(- 1.0);
const int INF = 0x3f3f3f3f;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
bool cmp(ll a, ll b){return a > b;}
//
int n, d;
vector<PII> sol;
vector<int> res;
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; ++ i){
int x; scanf("%d",&x);
sol.push_back(PII(x, i));
}
if(n <= 3){
printf("1\n");
return 0;
}
sort(sol.begin(), sol.end());
int tt = sol.size();
//1
d = sol[2].px - sol[1].px;
int flag = 0;
for(int i = 3; i < tt; ++ i){
if(sol[i].px - sol[i - 1].px != d){
flag = 1; break;
}
}
if(!flag){
printf("%d\n",sol[0].py);
return 0;
}
//2
flag = 0; d = sol[2].px - sol[0].px;
for(int i = 3; i < tt; ++ i){
if(sol[i].px - sol[i - 1].px != d){
flag = 1; break;
}
}
if(!flag){
printf("%d\n",sol[1].py);
return 0;
}
//3
flag = 0; d = sol[1].px - sol[0].px;
for(int i = 2; i < tt; ++ i){
if(sol[i].px - sol[i - 1].px != d) res.push_back(i);
}
tt = res.size();
if(tt > 2) printf("-1\n");
else if(tt == 1){
if(res[0] == n - 1) printf("%d\n",sol[res[0]].py);
else printf("-1\n");
}
else{
int t1 = res[0], t2 = res[1];
int tp1 = sol[t1].px - sol[t1 - 1].px;
int tp2 = sol[t2].px - sol[t2 - 1].px;
if(t2 - t1 != 1 || tp1 + tp2 != d) printf("-1\n");
else printf("%d\n",sol[t1].py);
}
return 0;
}
E - Polycarp and Snakes
题意:
一个人画蛇,每条蛇由一个小写字母组成,它只能是1 x l和 l x 1这两种样子,且字母大的可以覆盖小的。当出现一个字母时,比他小的字母蛇都画了。让你输出给的图满不满足要求,满足还要输出各条蛇的起始和结束位置。
分析:
我们可以先找到每个蛇的第一个位置,然后向左,向下扩展更新。同时记录没个字符的数量,用来判断这条蛇是不是1xl 或 l x 1的。如果一个字符没有出现,我们让变量tnum++,如果它后面的字符出现,我们就把这个字符的位置重复tnum+1次,认为最后这个字符把前面的都覆盖了。(见样例3)
再给几组数据理解:
3 2
..
.a
aa
>> NO
3 3
.aa
bb.
.a.
>> NO
代码:
#include<bits/stdc++.h>
using namespace std;
#define rep(i, l, r) for(long long i = l; i <= r; ++ i);
#define per(i, r, l) for(long long i = r; i >= l; -- i);
typedef long long ll;
typedef pair<int, int> PII;
const int N = 3e3 + 105;
const int mod = 998244353;
const double Pi = acos(- 1.0);
const ll INF = 1e18+1;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b & 1){ if(b) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
//
int n, m, T;
char s[N][N];
struct node{
int sx, sy, ex, ey;
}sol[50];
vector<node>res;
int cnum[50];
int main()
{
scanf("%d",&T);
while(T --){
scanf("%d%d",&n,&m);
for(int i = 0; i <= 25; ++ i) {
sol[i].sx = 0; cnum[i] = 0;
}
res.clear();
for(int i = 1; i <= n; ++ i){
scanf("%s",s[i] + 1);
for(int j = 1; j <= m; ++ j){
if(s[i][j] == '.') continue;
int tp = s[i][j] - 'a';
cnum[tp] ++;
if(!sol[tp].sx){
sol[tp] = (node){i, j, i, j};
}
}
}
int flag = 0, num = 0;
for(int z = 0; z <= 25; ++ z){
int tp = (char)('a' + z);
int x = sol[z].sx, y = sol[z].sy;
if(!x) {
num ++;
continue;
}
node e = (node){x, y, x, y};
int tx = x, ty = y;
int flag1 = 0, tnum = 0;
while(tx <= n){ //向下
if(s[tx][y] == tp){
tnum ++;
if(flag1){
flag = 1; break;
}
e.ex = tx;
}
else if(s[tx][y] == '.' || s[tx][y] < tp) flag1 = 1;
tx ++;
}
if(flag) break;
flag1 = 0;
while(ty <= m){ //向左
if(s[x][ty] == tp){
tnum ++;
if(flag1){
flag = 1; break;
}
e.ey = ty;
}
else if(s[x][ty] == '.' || s[x][ty] < tp) flag1 = 1;
ty ++;
}
if(e.ex != x && e.ey != y) flag = 1;
else if(tnum - 1 != cnum[z]) flag = 1;
if(flag) break;
while(num) {
res.push_back(e);
num --;
}
res.push_back(e);
}
if(flag) printf("NO\n");
else{
printf("YES\n");
int tt = res.size();
printf("%d\n",tt);
for(int i = 0; i < tt; ++ i){
printf("%d %d %d %d\n",res[i].sx,res[i].sy,res[i].ex,res[i].ey);
}
}
}
return 0;
}

