2020牛客暑期多校(七) C - A National Pandemic(树链剖分)
2020牛客暑期多校(七) C - A National Pandemic(树链剖分)
题意:
一棵树支持3种操作:
- 1 x w, 给x点加w,其它点y加 \(w-dist(x, y)\).
- 2 x, 将x权值变为$min(0, f(x)) $;
- 3 x, 查询x的权值\(f(x)\)
分析:
先推荐一个题单: 树链剖分练习题 如果没有学过树链剖分可以做一下。
首先2, 3操作用树链剖分处理都很直接,主要看1操作。给一个点x加w也还好处理,但给其他点加\(w - dist(x, y)\) 怎么加,难道要枚举点吗?显然点那么多会T。所以要处理这个操作可以观察这个式子可以写成 \(w - dist(1, x) - dist(1, y) + 2*dist(1, lca(x,y))\) 理解见下图,紫色是dist(1,x),绿色是dist(1, y) ,黄色是dist(1, lca(x,y))。
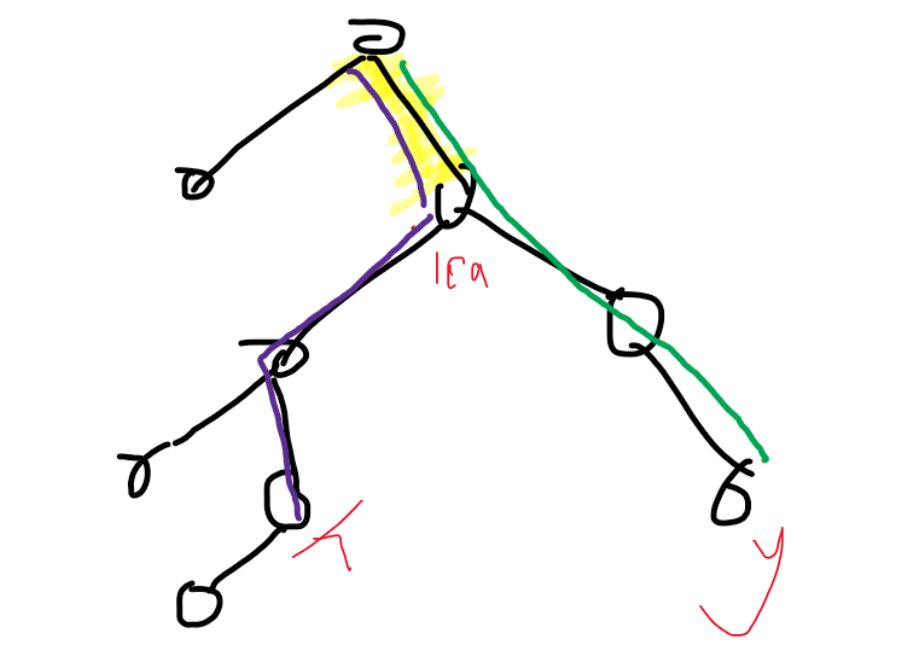
\(w - dist(1, x) - dist(1, y) + 2*dist(1, lca(x,y))\)
观察式子可以看到\(w-dist(1,x)\) 和 \(dist(1,y)\) 都可以用变量去累计,因为对一个查询3操作,它前面的1操作时的\(w-dist(1,x)\) 你可以累计下来,然后减\(dist(1, y)\) 的个数就是前面1操作的个数,也可以用一个变量allnum记录树量。
所以重点在处理\(dist(1,lca(x,y))\) 我们发现当查询一个点y时只要找到1到 y 路径上所以以前1操作标记的$lca(x,y) $点 ,求和这些点到 1 的距离即可,但这很麻烦不好处理。但是它是lca点到1的距离,所以我们可以在1处理时对1到x每个点权值+1,比如上图中处理x时,我把紫线上所有点+1,那么当处理2时我想要加的是1到lca的距离,可以发现此时1到lca的权值和就是1到lca的距离,这里用了差分的一个思想。当我们有很多x时,它们会在1到y条路径上1到某个点之间权值都加1,其实这个点就是lca,这个很好理解。所以我们只要用线段树维护权值和即可。但我们观察式子要2*dist(1,lca(x,y)).这只需要对每个1操作的x给线段树1到x之间的点+2即可。
代码:
#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i);
#define per(i, a, n) for(int i = n; i >= a; -- i);
typedef long long ll;
const int N = 50010;
const ll mod = 1e9 + 7;
const double Pi = acos(- 1.0);
const int INF = 0x3f3f3f3f;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
ll lcm(ll a, ll b) { return a * b / gcd(a, b);}
bool cmp(int a, int b){ return a > b;}
//
int T, n, m;
int head[N << 1], cnt = 0;
struct node{
int to, nxt;
}edge[N * 4];
struct Tree{
int l, r; int val, lz;
}tree[N * 4];
int del[N];
int son[N], dfn[N], dep[N], top[N], fa[N], siz[N];
int tot;
void add(int u, int v){
edge[cnt].to = v, edge[cnt].nxt = head[u], head[u] = cnt ++;
edge[cnt].to = u, edge[cnt].nxt = head[v], head[v] = cnt ++;
}
void pushdown(int index){
if(tree[index].lz){
int temp = tree[index].lz;
tree[index].lz = 0;
tree[index << 1].val += (tree[index << 1].r - tree[index << 1].l + 1) * temp;
tree[index << 1 | 1].val += (tree[index << 1 | 1].r - tree[index << 1 | 1].l + 1) * temp;
tree[index << 1].lz += temp;
tree[index << 1 | 1].lz += temp;
}
}
void Build(int l, int r, int index){
tree[index].l = l, tree[index].r = r;
tree[index].lz = 0;
if(l == r){
tree[index].val = 0;
return;
}
int mid = (tree[index].l + tree[index].r) >> 1;
Build(l, mid, index << 1);
Build(mid + 1, r, index << 1 | 1);
tree[index].val = tree[index << 1].val + tree[index << 1 | 1].val;
}
void updata(int l, int r, int index, int val){
if(tree[index].l >= l && tree[index].r <= r){
tree[index].lz += val;
tree[index].val += val * (tree[index].r - tree[index].l + 1);
return;
}
if(tree[index].lz) pushdown(index);
int mid = (tree[index].l + tree[index].r) >> 1;
if(l <= mid) updata(l, r, index << 1, val);
if(r > mid) updata(l, r, index << 1 | 1, val);
tree[index].val = tree[index << 1].val + tree[index << 1 | 1].val;
}
int query(int l, int r, int index){
if(l <= tree[index].l && tree[index].r <= r){
return tree[index].val;
}
if(tree[index].lz) pushdown(index);
int mid = (tree[index].l + tree[index].r) >> 1;
int ans = 0;
if(l <= mid) ans += query(l, r, index << 1);
if(r > mid) ans += query(l, r, index << 1 | 1);
return ans;
}
// -------------------------------------
void Csol(int x, int y){
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]]) swap(x, y);
updata(dfn[top[x]], dfn[x], 1, 2);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
updata(dfn[x], dfn[y], 1, 2);
}
int Qsol(int x, int y){
int ans = 0;
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]]) swap(x, y);
ans += query(dfn[top[x]], dfn[x], 1);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x ,y);
ans += query(dfn[x], dfn[y], 1);
return ans;
}
void dfs1(int u, int pre){
dep[u] = dep[pre] + 1;
fa[u] = pre;
siz[u] = 1;
int maxx = -1;
for(int i = head[u]; i != -1; i = edge[i].nxt){
int v = edge[i].to;
if(v == pre) continue;
dfs1(v, u);
siz[u] += siz[v];
if(siz[v] > maxx){
maxx = siz[v];
son[u] = v;
}
}
}
void dfs2(int u, int topu){ //topu当前链的最顶端的节点
dfn[u] = ++ tot;
top[u] = topu;
if(!son[u]) return;
dfs2(son[u], topu);
for(int i = head[u]; i != -1; i = edge[i].nxt){
int v = edge[i].to;
if(v == son[u] || v == fa[u]) continue;
dfs2(v, v);
}
}
int main()
{
scanf("%d",&T);
while(T --){
scanf("%d%d",&n,&m);
cnt = 0; tot = 0;
for(int i = 1; i <= n; ++ i){
head[i] = -1; del[i] = 0;
son[i] = 0;
}
int x, y;
for(int i = 1; i < n; ++ i){
scanf("%d%d",&x,&y);
add(x, y);
}
dep[0] = 0;
dfs1(1, 0);
dfs2(1, 1);
Build(1, n, 1);
int op;
int wval = 0, allnum = 0;
while(m --){
scanf("%d",&op);
if(op == 1){
scanf("%d%d",&x,&y);
Csol(x, 1);
wval = wval + y - dep[x];
allnum ++;
}
else if(op == 2){
scanf("%d",&x);
int res = Qsol(x, 1) + wval - allnum * dep[x];
if(res > del[x]) del[x] = res;
}
else{
scanf("%d",&x);
int res = Qsol(x, 1) + wval - allnum * dep[x] - del[x];
printf("%d\n",res);
}
}
}
return 0;
}


