HDU6865 杭电多校8 1011-Kidnapper's Matching Problem (线性基+KMP)

HDU6865 杭电多校8 1011-Kidnapper's Matching Problem (线性基+KMP)

题意：

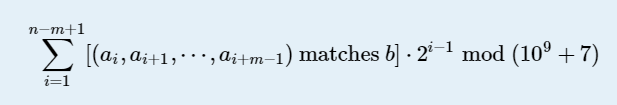
题意就是计算这个式子，[condition] 当\(a_{i} ... a_{i+m-1}​\) 与b数组满足匹配关系时为1。具体匹配关系指\(a_{i} \oplus b_{i} \in 2^{S}_{⊕}​\) 。其中 S 为输入的一组数，$ 2^{S}_{⊕}​$ 表示S数组所有任意子集的异或和结果的集合。

题解：

这里先放题解原文：

具体就是先用 S 数组计算其线性基，得到$ 2^{S}_{⊕}$ 。 然后按题解的结论把a[], b[]数组中的数去掉线性基中有的位得到 \(a`[\ ] ，b`[\ ]\)。然后找能够按题意匹配的位置 i ，当然按照题解结论，对匹配的那一段有 \(a`[i] = b`[i]\) 。 所以直接用KMP去处理就好了。

代码：

#include<bits/stdc++.h>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i)
#define per(i, a, n) for(int i = n; i >= a; -- i)
typedef long long ll;
const int N = 2e6 + 105;
const int mod = 1e9 + 7;
const double Pi = acos(- 1.0);
const ll INF = 1e18;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
//

const int maxbit = 62;		//maxbit不能太大

struct L_B{
	ll lba[maxbit], p[maxbit];
	int cnt;
	L_B(){
        memset(lba, 0, sizeof(lba));
        memset(p, 0, sizeof(p));
        cnt = 0;
    }
    
	void Insert(ll val){		//插入
        for(int i = maxbit - 1; i >= 0; -- i)
            if(val & (1ll << i)){
                if(!lba[i]){
                    lba[i] = val;
                    break;
                }
                val ^= lba[i];
            }
    }
};
// --------------线性基模板



int T, n, m, k;
ll a[N], b[N];
int nxt[N];
int vis[N];

void get_next()
{
    int i = 1, j = 0;
    nxt[1] = 0;
    while(i <= m){
        if(j == 0 || b[i] == b[j]){
            i ++, j ++, nxt[i] = j;
        }
        else j = nxt[j];
    }
}

void KMP()
{
    get_next();
    int i = 0, j = 0;
    while(i <= n && j <= m){
        if(j == 0 || a[i] == b[j]) i++, j++;
        else j = nxt[j];
        
        if(j == m + 1){
            vis[i - m] = 1;
            j = nxt[j];
        }
    }
}

void init(){
    for(int i = 0; i <= n; ++ i){
        nxt[i] = 0; vis[i] = 0;
    }
}

int main()
{
    scanf("%d",&T);
    while(T --){
        L_B lb;
        scanf("%d%d%d",&n,&m,&k);
        for(int i = 1; i <= n; ++ i) scanf("%d",&a[i]);
        for(int i = 1; i <= m; ++ i) scanf("%d",&b[i]);
        for(int i = 1; i <= k; ++ i){
            ll x; scanf("%lld",&x);
            lb.Insert(x);
        }
        for(int i = 1; i <= n; ++ i){
            for(int j = maxbit - 1; j >= 0; -- j){
                if(a[i] & (1 << j)){
                    a[i] ^= lb.lba[j];
                }
            }
        }
        for(int i = 1; i <= m; ++ i){
            for(int j = maxbit - 1; j >= 0; -- j){
                if(b[i] & (1 << j)){
                    b[i] ^= lb.lba[j];
                }
            }
        }

        init(); KMP();
        ll res = 0, temp = 1;
        for(int i = 1; i <= n - m + 1; ++ i){
            if(vis[i]) res = (res + temp) % mod;
            temp = temp * 2ll % mod;
        }
        printf("%lld\n",res);
    }
    return 0;
}